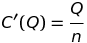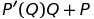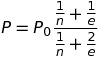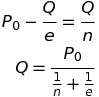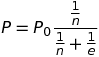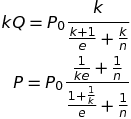game theory

The Prisoner’s Dilemma

PNRJ core principles, critique of neoclassical economics , , , , , ,

JDN 2457348
When this post officially goes live, it will have been one full week since I launched my Patreon, on which I’ve already received enough support to be more than halfway to my first funding goal. After this post, I will be far enough ahead in posting that I can release every post one full week ahead of time for my Patreon patrons (can I just call them Patreons?).

It’s actually fitting that today’s topic is the Prisoner’s Dilemma, for Patreon is a great example of how real human beings can find solutions to this problem even if infinite identical psychopaths could not.

The Prisoner’s Dilemma is the most fundamental problem in game theory—arguably the reason game theory is worth bothering with in the first place. There is a standard story that people generally tell to set up the dilemma, but honestly I find that they obscure more than they illuminate. You can find it in the Wikipedia article if you’re interested.

The basic idea of the Prisoner’s Dilemma is that there are many times in life when you have a choice: You can do the nice thing and cooperate, which costs you something, but benefits the other person more; or you can do the selfish thing and defect, which benefits you but harms the other person more.

The game can basically be defined as four possibilities: If you both cooperate, you each get 1 point. If you both defect, you each get 0 points. If you cooperate when the other player defects, you lose 1 point while the other player gets 2 points. If you defect when the other player cooperates, you get 2 points while the other player loses 1 point.

P2 Cooperate P2 Defect
P1 Cooperate +1, +1 -1, +2
P2 Defect +2, -1 0, 0

These games are nonzero-sum, meaning that the total amount of benefit or harm incurred is not constant; it depends upon what players choose to do. In my example, the total benefit varies from +2 (both cooperate) to +1 (one cooperates, one defects) to 0 (both defect).

The answer which is “neat, plausible, and wrong” (to use Mencken’s oft-misquoted turn of phrase) is to reason this way: If the other player cooperates, I can get +1 if I cooperate, or +2 if I defect. So I should defect. If the other player defects, I can get -1 if I cooperate, or 0 if I defect. So I should defect. In either case I defect, therefore I should always defect.

The problem with this argument is that your behavior affects the other player. You can’t simply hold their behavior fixed when making your choice. If you always defect, the other player has no incentive to cooperate, so you both always defect and get 0. But if you credibly promise to cooperate every time they also cooperate, you create an incentive to cooperate that can get you both +1 instead.

If there were a fixed amount of benefit, the game would be zero-sum, and cooperation would always be damaging yourself. In zero-sum games, the assumption that acting selfishly maximizes your payoffs is correct; we could still debate whether it’s necessarily more rational (I don’t think it’s always irrational to harm yourself to benefit someone else an equal amount), but it definitely is what maximizes your money.

But in nonzero-sum games, that assumption no longer holds; we can both end up better off by cooperating than we would have been if we had both defected.
Below is a very simple zero-sum game (notice how indeed in each outcome, the payoffs sum to zero; any zero-sum game can be written so that this is so, hence the name):

Player 2 cooperates Player 2 defects
Player 1 cooperates 0, 0 -1, +1
Player 1 defects +1, -1 0, 0

In that game, there really is no reason for you to cooperate; you make yourself no better off if they cooperate, and you give them a strong incentive to defect and make you worse off. But that game is not a Prisoner’s Dilemma, even though it may look superficially similar.

The real world, however, is full of variations on the Prisoner’s Dilemma. This sort of situation is fundamental to our experience; it probably happens to you multiple times every single day.
When you finish eating at a restaurant, you could pay the bill (cooperate) or you could dine and dash (defect). When you are waiting in line, you could quietly take your place in the queue (cooperate) or you could cut ahead of people (defect). If you’re married, you could stay faithful to your spouse (cooperate) or you could cheat on them (defect). You could pay more for the shoes made in the USA (cooperate), or buy the cheap shoes that were made in a sweatshop (defect). You could pay more to buy a more fuel-efficient car (cooperate), or buy that cheap gas-guzzler even though you know how much it pollutes (defect). Most of us cooperate most of the time, but occasionally are tempted into defecting.

The “Prisoner’s Dilemma” is honestly not much of a dilemma. A lot of neoclassical economists really struggle with it; their model of rational behavior is so narrow that it keeps putting out the result that they are supposed to always defect, but they know that this results in a bad outcome. More recently we’ve done experiments and we find that very few people actually behave that way (though typically neoclassical economists do), and also that people end up making more money in these experimental games than they would if they behaved as neoclassical economics says would be optimal.

Let me repeat that: People make more money than they would if they acted according to what’s supposed to be optimal according to neoclassical economists. I think that’s why it feels like such a paradox to them; their twin ideals of infinite identical psychopaths and maximizing the money you make have shown themselves to be at odds with one another.

But in fact, it’s really not that paradoxical: Rationality doesn’t mean being maximally selfish at every opportunity. It also doesn’t mean maximizing the money you make, but even if it did, it still wouldn’t mean being maximally selfish.

We have tested experimentally what sort of strategy is most effective at making the most money in the Prisoner’s Dilemma; basically we make a bunch of competing computer programs to play the game against one another for points, and tally up the points. When we do that, the winner is almost always a remarkably simple strategy, called “Tit for Tat”. If your opponent cooperated last time, cooperate. If your opponent defected last time, defect. Reward cooperation, punish defection.

In more complex cases (such as allowing for random errors in behavior), some subtle variations on that strategy turn out to be better, but are still basically focused around rewarding cooperation and punishing defection.
This probably seems quite intuitive, yes? It may even be the strategy that it occurred to you to try when you first learned about the game. This strategy comes naturally to humans, not because it is actually obvious as a mathematical result (the obvious mathematical result is the neoclassical one that turns out to be wrong), but because it is effective—human beings evolved to think this way because it gave us the ability to form stable cooperative coalitions. This is what gives us our enormous evolutionary advantage over just about everything else; we have transcended the limitations of a single individual and now work together in much larger groups. E.O. Wilson likes to call us “eusocial”, a term formally applied only to a very narrow range of species such as ants and bees (and for some reason, naked mole rats); but I don’t think this is actually strong enough, because human beings are social in a way that even ants are not. We cooperate on the scale of millions of individuals, who are basically unrelated genetically (or very distantly related). That is what makes us the species who eradicate viruses and land robots on other planets. Much more so than intelligence per se, the human superpower is cooperation.

Indeed, it is not a great exaggeration to say that morality exists as a concept in the human mind because cooperation is optimal in many nonzero-sum games such as these. If the world were zero-sum, morality wouldn’t work; the immoral action would always make you better off, and the bad guys would always win. We probably would never even have evolved to think in moral terms, because any individual or species that started to go that direction would be rapidly outcompeted by those that remained steadfastly selfish.

Monopoly and Oligopoly

PNRJ core principles, Top 10 things to know about economics , , , , , , , , , , , ,

JDN 2457180 EDT 08:49

Welcome to the second installment in my series, “Top 10 Things to Know About Economics.” The first was not all that well-received, because it turns it out it was just too dense with equations (it didn’t help that the equation formatting was a pain.) Fortunately I think I can explain monopoly and oligopoly with far fewer equations—which I will represent as PNG for your convenience.

You probably already know at least in basic terms how a monopoly works: When there is only one seller of a product, that seller can charge higher prices. But did you ever stop and think about why they can charge higher prices—or why they’d want to?

The latter question is not as trivial as it sounds; higher prices don’t necessarily mean higher profits. By the Law of Demand (which, like the Pirate Code, is really more like a guideline), raising the price of a product will result in fewer being sold. There are two countervailing effects: Raising the price raises the profits from selling each item, but reduces the number of items sold. The optimal price, therefore, is the one that balances these two effects, maximizing price times quantity.

A monopoly can actually set this optimal price (provided that they can figure out what it is, of course; but let’s assume they can). They therefore solve this maximization problem for price P(Q) a function of quantity sold, quantity Q, and cost C(Q) a function of quantity produced (which at the optimum is equal to quantity sold; no sense making them if you won’t sell them!):

monopoly_optimization

As you may remember if you’ve studied calculus, the maximum is achieved at the point where the derivative is zero. If you haven’t studied calculus, the basic intuition here is that you move along the curve seeing whether the profits go up or down with each small change, and when you reach the very top—the maximum—you’ll be at a point where you switch from going up to going down, and at that exact point a small change will move neither up nor down. The derivative is really just a fancy term for the slope of the curve at each point; at a maximum this slope changes from positive to negative, and at the exact point it is zero.

derivative_maximum

monopoly_general

This is a general solution, but it’s easier to understand if we use something more specific. As usual, let’s make things simpler by assuming everything is linear; we’ll assume that demand starts at a maximum price of P0 and then decreases at a rate 1/e. This is the demand curve.

linear_demand

Then, we’ll assume that the marginal cost of production C'(Q) is also linear, increasing at a rate 1/n. This is the supply curve.

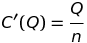
linear_supply

Now we can graph the supply and demand curves from these equations. But the monopoly doesn’t simply set supply equal to demand; instead, they set supply equal to marginal revenue, which takes into account the fact that selling more items requires lowering the price on all of them. Marginal revenue is this term:

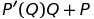
marginal_revenue

This is strictly less than the actual price, because increasing the quantity sold requires decreasing the price—which means that P'(Q) < 0. They set the quantity by setting marginal revenue equal to marginal cost. Then they set the price by substituting that quantity back into the demand equation.

Thus, the monopoly should set this quantity:

linear_monopoly_solution

They would then charge this price (substitute back into the demand equation):

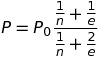
linear_monopoly_price

On a graph, there are the supply and demand curves, and then below the demand curve, the marginal revenue curve; it’s the intersection of that curve with the supply curve that the monopoly uses to set its quantity, and then it substitutes that quantity into the demand curve to get the price:

elastic_supply_monopolistic_labeled

Now I’ll show that this is higher than the price in a perfectly competitive market. In a competitive market, competitive companies can’t do anything to change the price, so from their perspective P'(Q) = 0. They can only control the quantity they produce and sell; they keep producing more as long as they receive more money for each one than it cost to produce it. By the Law of Diminishing Returns (again more like a guideline) the cost will increase as they produce more, until finally the last one they sell cost just as much to make as they made from selling it. (Why bother selling that last one, you ask? You’re right; they’d actually sell one less than this, but if we assume that we’re talking about thousands of products sold, one shouldn’t make much difference.)

Price is simply equal to marginal cost:

perfect_competition_general

In our specific linear case that comes out to this quantity:

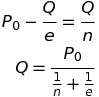
linear_competitive_solution

Therefore, they charge this price (you can substitute into either the supply or demand equations, because in a competitive market supply equals demand):

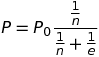
linear_competitive_price

Subtract the two, and you can see that monopoly price is higher than the competitive price by this amount:

linear_monopoly_premium

Notice that the monopoly price will always be larger than the competitive price, so long as e > 0 and n > 0, meaning that increasing the quantity sold requires decreasing the price, but increasing the cost of production. A monopoly has an incentive to raise the price higher than the competitive price, but not too much higher—they still want to make sure they sell enough products.

Monopolies introduce deadweight loss, because in order to hold the price up they don’t produce as many products as people actually want. More precisely, each new product produced would add overall value to the economy, but the monopoly stops producing them anyway because it wouldn’t add to their own profits.

One “solution” to this problem is to let the monopoly actually take those profits; they can do this if they price-discriminate, charging a higher price for some customers than others. In the best-case scenario (for them), they charge each customer a price that they are just barely willing to pay, and thus produce until no customer is willing to pay more than the product costs to make. That final product sold also has price equal to marginal cost, so the total quantity sold is the same under competition. It is, in that sense, “efficient”.

What many neoclassical economists seem to forget about price-discriminating monopolies is that they appropriate the entire surplus value of the product—the customers are only just barely willing to buy; they get no surplus value from doing so.

In reality, very few monopolies can price-discriminate that precisely; instead, they put customers into broad categories and then try to optimize the price for each of those categories. Credit ratings, student discounts, veteran discounts, even happy hours are all forms of this categorical price discrimination. If the company cares even a little bit about what sort of customer you are rather than how much money you’re paying, they are price-discriminating.

It’s so ubiquitous I’m actually having trouble finding a good example of a product that doesn’t have categorical price discrimination. I was thinking maybe computers? Nope, student discounts. Cars? No, employee discounts and credit ratings. Refrigerators, maybe? Well, unless there are coupons (coupons price discriminate against people who don’t want to bother clipping them). Certainly not cocktails (happy hour) or haircuts (discrimination by sex, the audacity!); and don’t even get me started on software.

I introduced price-discrimination in the context of monopoly, which is usually how it’s done; but one thing you’ll notice about all the markets I just indicated is that they aren’t monopolies, yet they still exhibit price discrimination. Cars, computers, refrigerators, and software are made under oligopoly, a system in which a handful of companies control the majority of the market. As you might imagine, an oligopoly tends to act somewhere in between a monopoly and a competitive market—but there are some very interesting wrinkles I’ll get to in a moment.

Cocktails and haircuts are sold in a different but still quite interesting system called monopolistic competition; indeed, I’m not convinced that there is any other form of competition in the real world. True perfectly-competitive markets just don’t seem to actually exist. Under monopolistic competition, there are many companies that don’t have much control over price in the overall market, but the products they sell aren’t quite the same—they’re close, but not equivalent. Some barbers are just better at cutting hair, and some bars are more fun than others. More importantly, they aren’t the same for everyone. They have different customer bases, which may overlap but still aren’t the same. You don’t just want a barber who is good, you want one who works close to where you live. You don’t just want a bar that’s fun; you want one that you can stop by after work. Even if you are quite discerning and sensitive to price, you’re not going to drive from Ann Arbor to Cleveland to get your hair cut—it would cost more for the gasoline than the difference. And someone is Cleveland isn’t going to drive all the way to Ann Arbor, either! Hence, barbers in Ann Arbor have something like a monopoly (or oligopoly) over Ann Arbor haircuts, and barbers in Cleveland have something like a monopoly over Cleveland haircuts. That’s monopolistic competition.

Supposedly monopolistic competition drives profits to zero in the long run, but I’ve yet to see this happen in any real market. Maybe the problem is that conceit “the long run”; as Keynes said, “in the long run we are all dead.” Sometimes the argument is made that it has driven real economic profits to zero, because you’ve got to take into account the cost of entry, the normal profit. But of course, that’s extremely difficult to measure, so how do we know whether profits have been driven to normal profit? Moreover, the cost of entry isn’t the same for everyone, so people with lower cost of entry are still going to make real economic profits. This means that the majority of companies are going to still make some real economic profit, and only the ones that had the hardest time entering will actually see their profits driven to zero.

Monopolistic competition is relatively simple. Oligopoly, on the other hand, is fiercely complicated. Why? Because under oligopoly, you actually have to treat human beings as human beings.

What I mean by that is that under perfect competition or even monopolistic competition, the economic incentives are so powerful that people basically have to behave according to the neoclassical rational agent model, or they’re going to go out of business. There is very little room for errors or even altruistic acts, because your profit margin is so tight. In perfect competition, there is literally zero room; in monopolistic competition, the only room for individual behavior is provided by the degree of monopoly, which in most industries is fairly small. One person’s actions are unable to shift the direction of the overall market, so the market as a system has ultimate power.

Under oligopoly, on the other hand, there are a handful of companies, and people know their names. You as a CEO have a reputation with customers—and perhaps more importantly, a reputation with other companies. Individual decision-makers matter, and one person’s decision depends on their prediction of other people’s decision. That means we need game theory.

The simplest case is that of duopoly, where there are only two major companies. Not many industries are like this, but I can think of three: soft drinks (Coke and Pepsi), commercial airliners (Boeing and Airbus), and home-user operating systems (Microsoft and Apple). In all three cases, there is also some monopolistic element, because the products they sell are not exactly the same; but for now let’s ignore that and suppose they are close enough that nobody cares.

Imagine yourself in the position of, say, Boeing: How much should you charge for an airplane?

If Airbus didn’t exist, it’s simple; you’d charge the monopoly price. But since they do exist, the price you charge must depend not only on the conditions of the market, but also what you think Airbus is likely to do—and what they are likely to do depends in turn on what they think you are likely to do.

If you think Airbus is going to charge the monopoly price, what should you do? You could charge the monopoly price as well, which is called collusion. It’s illegal to actually sign a contract with Airbus to charge that price (though this doesn’t seem to stop cable companies or banks—probably has something to do with the fact that we never punish them for doing it), and let’s suppose you as the CEO of Boeing are an honest and law-abiding citizen (I know, it’s pretty fanciful; I’m having trouble keeping a straight face myself) and aren’t going to violate the antitrust laws. You can still engage in tacit collusion, in which you both charge the monopoly price and take your half of the very high monopoly profits.

There’s a temptation not to collude, however, which the airlines who buy your planes are very much hoping you’ll succumb to. Suppose Airbus is selling their A350-100 for $341 million. You could sell the comparable 777-300ER for $330 million and basically collude, or you could cut the price and draw in more buyers. Say you cut it to $250 million; it probably only costs $150 million to make, so you’re still making a profit on each one; but where you sold say 150 planes a year and profited $180 million on each (a total profit of $27 billion), you could instead capture the whole market and sell 300 planes a year and profit $100 million on each (a total profit of $30 billion). That’s a 10% higher profit and $3 billion a year for your shareholders; why wouldn’t you do that?

Well, think about what will happen when Airbus releases next year’s price list. You cut the price to $250 million, so they retaliate by cutting their price to $200 million. Next thing you know, you’re cutting your own price to $150.1 million just to stay in the market, and they’re doing the same. When the dust settles, you still only control half the market, but now you profit a mere $100,000 per airplane, making your total profits a measly $15 million instead of $27 billion—that’s $27,000 million. (I looked it up, and as it turns out, Boeing’s actual gross profit is about $14 billion, so I underestimated the real cost of each airplane—but they’re clearly still colluding.) For a gain of 10% in one year you’ve paid a loss of 99.95% indefinitely. The airlines will be thrilled, and they’ll likely pass on much of those savings to their customers, who will fly more often, engage in more tourism, and improve the economy in tourism-dependent countries like France and Greece, so the world may well be better off. But you as CEO of Boeing don’t care about the world; you care about the shareholders of Boeing—and the shareholders of Boeing just got hosed. Don’t expect to keep your seat in the next election.

But now, suppose you think that Airbus is planning on setting a price of $250 million next year anyway. They should know you’ll retaliate, but maybe their current CEO is retiring next year and doesn’t care what happens to the company after that or something. Or maybe they’re just stupid or reckless. In any case, your sources (which, as an upstanding citizen, obviously wouldn’t include any industrial espionage!) tell you that Airbus is going to charge $250 million next year.

Well, in that case there’s no point in you charging $330 million; you’ll lose the market and look like a sucker. You could drop to $250 million and try to set up a new, lower collusive equilibrium; but really what you want to do is punish them severely for backstabbing you. (After all, human beings are particularly quick to anger when we perceive betrayal. So maybe you’ll charge $200 million and beat them at their own conniving game.

The next year, Airbus has a choice. They could raise back to $341 million and give you another year of big profits to atone for their reckless actions, or they could cut down to $180 million and keep the price war going. You might think that they should continue the war, but that’s short-term thinking; in the long run their best strategy is to atone for their actions and work to restore the collusion. In response, Boeing’s best strategy is to punish them when they break the collusion, but not hold a grudge; if they go back to the high price, Boeing should as well. This very simple strategy is called tit-for-tat, and it is utterly dominant in every simulation we’ve ever tried of this situation, which is technically called an iterated prisoner’s dilemma.

What if there are more than two companies involved? Then things get even more complicated, because now we’re dealing with things like what A’s prediction of what B predicts that C will predict A will do. In general this is a situation we only barely understand, and I think it is a topic that needs considerably more research than it has received.

There is an interesting simple model that actually seems to capture a lot about how oligopolies work, but no one can quite figure out why it works. That model is called Cournot competition. It assumes that companies take prices and fixed and compete by selecting the quantity they produce at each cycle. That’s incredibly bizarre; it seems much more realistic to say that they compete by setting prices. But if you do that, you get Bertrand competition, which requires us to go through that whole game-theory analysis—but now with three, or four, or ten companies!

Under Cournot competition, you decide how much to produce Q1 by monopolizing what’s left over after the other companies have produced their quantities Q2, Q3, and so on. If there are k companies, you optimize under the constraint that (k-1)Q2 has already been produced.

Let’s use our linear models again. Here, the quantity that goes into figuring the price is the total quantity, which is Q1+(k-1)Q2; while the quantity you sell is just Q1. But then, another weird part is that for the marginal cost function we use the whole market—maybe you’re limited by some natural resource, like oil or lithium?

It’s not as important for you to follow along with the algebra, though here you go if you want:

linear_Cournot_1

Then the key point is that the situation is symmetric, so Q1 = Q2 = Q3 = Q. Then the total quantity produced, which is what consumers care about, is kQ. That’s what sets the actual price as well.

linear_Cournot_2

The two equations to focus on are these ones:

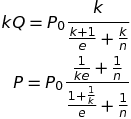
linear_Cournot_3

If you plug in k=1, you get a monopoly. If you take the limit as k approaches infinity, you get perfect competition. And in between, you actually get a fairly accurate representation of how the number of companies in an industry affects the price and quantity sold! From some really bizarre assumptions about how competition works! The best explanation I’ve seen of why this might happen is this 1983 paper showing that price competition can behave like Cournot competition if companies have to first commit to producing a certain quantity before naming their prices.

But of course, it doesn’t always give an accurate representation of oligopoly, and for that we’ll probably need a much more sophisticated multiplayer game theory analysis which has yet to be done.

And that, dear readers, is how monopoly and oligopoly raise prices.

Pareto Efficiency: Why we need it—and why it’s not enough

PNRJ core principles, critique of neoclassical economics, Top 10 things to know about economics , , , , , , , , , , , , , , , ,

JDN 2456914 PDT 11:45.

I already briefly mentioned the concept in an earlier post, but Pareto-efficiency is so fundamental to both ethics and economics I decided I would spent some more time on explaining exactly what it’s about.

This is the core idea: A system is Pareto-efficient if you can’t make anyone better off without also making someone else worse off. It is Pareto-inefficient if the opposite is true, and you could improve someone’s situation without hurting anyone else.

Improving someone’s situation without harming anyone else is called a Pareto-improvement. A system is Pareto-efficient if and only if there are no possible Pareto-improvements.

Zero-sum games are always Pareto-efficient. If the game is about how we distribute the same $10 between two people, any dollar I get is a dollar you don’t get, so no matter what we do, we can’t make either of us better off without harming the other. You may have ideas about what the fair or right solution is—and I’ll get back to that shortly—but all possible distributions are Pareto-efficient.

Where Pareto-efficiency gets interesting is in nonzero-sum games. The most famous and most important such game is the so-called Prisoner’s Dilemma; I don’t like the standard story to set up the game, so I’m going to give you my own. Two corporations, Alphacomp and Betatech, make PCs. The computers they make are of basically the same quality and neither is a big brand name, so very few customers are going to choose on anything except price. Combining labor, materials, equipment and so on, each PC costs each company $300 to manufacture a new PC, and most customers are willing to buy a PC as long as it’s no more than $1000. Suppose there are 1000 customers buying. Now the question is, what price do they set? They would both make the most profit if they set the price at $1000, because customers would still buy and they’d make $700 on each unit, each making $350,000. But now suppose Alphacomp sets a price at $1000; Betatech could undercut them by making the price $999 and sell twice as many PCs, making $699,000. And then Alphacomp could respond by setting the price at $998, and so on. The only stable end result if they are both selfish profit-maximizers—the Nash equilibrium—is when the price they both set is $301, meaning each company only profits $1 per PC, making $1000. Indeed, this result is what we call in economics perfect competition. This is great for consumers, but not so great for the companies.

If you focus on the most important choice, $1000 versus $999—to collude or to compete—we can set up a table of how much each company would profit by making that choice (a payoff matrix or normal form game in game theory jargon).

A: $999 A: $1000
B: $999 A:$349k

B:$349k

 A:$0

B:$699k
B: $1000 A:$699k

B:$0

 A:$350k

B:$350k

Obviously the choice that makes both companies best-off is for both companies to make the price $1000; that is Pareto-efficient. But it’s also Pareto-efficient for Alphacomp to choose $999 and the other one to choose $1000, because then they sell twice as many computers. We have made someone worse off—Betatech—but it’s still Pareto-efficient because we couldn’t give Betatech back what they lost without taking some of what Alphacomp gained.

There’s only one option that’s not Pareto-efficient: If both companies charge $999, they could both have made more money if they’d charged $1000 instead. The problem is, that’s not the Nash equilibrium; the stable state is the one where they set the price lower.

This means that only case that isn’t Pareto-efficient is the one that the system will naturally trend toward if both compal selfish profit-maximizers. (And while most human beings are nothing like that, most corporations actually get pretty close. They aren’t infinite, but they’re huge; they aren’t identical, but they’re very similar; and they basically are psychopaths.)

In jargon, we say the Nash equilibrium of a Prisoner’s Dilemma is Pareto-inefficient. That one sentence is basically why John Nash was such a big deal; up until that point, everyone had assumed that if everyone acted in their own self-interest, the end result would have to be Pareto-efficient; Nash proved that this isn’t true at all. Everyone acting in their own self-interest can doom us all.

It’s not hard to see why Pareto-efficiency would be a good thing: if we can make someone better off without hurting anyone else, why wouldn’t we? What’s harder for most people—and even most economists—to understand is that just because an outcome is Pareto-efficient, that doesn’t mean it’s good.

I think this is easiest to see in zero-sum games, so let’s go back to my little game of distributing the same $10. Let’s say it’s all within my power to choose—this is called the ultimatum game. If I take $9 for myself and only give you $1, is that Pareto-efficient? It sure is; for me to give you any more, I’d have to lose some for myself. But is it fair? Obviously not! The fair option is for me to go fifty-fifty, $5 and $5; and maybe you’d forgive me if I went sixty-forty, $6 and $4. But if I take $9 and only offer you $1, you know you’re getting a raw deal.

Actually as the game is often played, you have the choice the say, “Forget it; if that’s your offer, we both get nothing.” In that case the game is nonzero-sum, and the choice you’ve just taken is not Pareto-efficient! Neoclassicists are typically baffled at the fact that you would turn down that free $1, paltry as it may be; but I’m not baffled at all, and I’d probably do the same thing in your place. You’re willing to pay that $1 to punish me for being so stingy. And indeed, if you allow this punishment option, guess what? People aren’t as stingy! If you play the game without the rejection option, people typically take about $7 and give about $3 (still fairer than the $9/$1, you may notice; most people aren’t psychopaths), but if you allow it, people typically take about $6 and give about $4. Now, these are pretty small sums of money, so it’s a fair question what people might do if $100,000 were on the table and they were offered $10,000. But that doesn’t mean people aren’t willing to stand up for fairness; it just means that they’re only willing to go so far. They’ll take a $1 hit to punish someone for being unfair, but that $10,000 hit is just too much. I suppose this means most of us do what Guess Who told us: “You can sell your soul, but don’t you sell it too cheap!”

Now, let’s move on to the more complicated—and more realistic—scenario of a nonzero-sum game. In fact, let’s make the “game” a real-world situation. Suppose Congress is debating a bill that would introduce a 70% marginal income tax on the top 1% to fund a basic income. (Please, can we debate that, instead of proposing a balanced-budget amendment that would cripple US fiscal policy indefinitely and lead to a permanent depression?)

This tax would raise about 14% of GDP in revenue, or about $2.4 trillion a year (yes, really). It would then provide, for every man, woman and child in America, a $7000 per year income, no questions asked. For a family of four, that would be $28,000, which is bound to make their lives better.

But of course it would also take a lot of money from the top 1%; Mitt Romney would only make $6 million a year instead of $20 million, and Bill Gates would have to settle for $2.4 billion a year instead of $8 billion. Since it’s the whole top 1%, it would also hurt a lot of people with more moderate high incomes, like your average neurosurgeon or Paul Krugman, who each make about $500,000 year. About $100,000 of that is above the cutoff for the top 1%, so they’d each have to pay about $70,000 more than they currently do in taxes; so if they were paying $175,000 they’re now paying $245,000. Once taking home $325,000, now only $255,000. (Probably not as big a difference as you thought, right? Most people do not seem to understand how marginal tax rates work, as evinced by “Joe the Plumber” who thought that if he made $250,001 he would be taxed at the top rate on the whole amount—no, just that last $1.)

You can even suppose that it would hurt the economy as a whole, though in fact there’s no evidence of that—we had tax rates like this in the 1960s and our economy did just fine. The basic income itself would inject so much spending into the economy that we might actually see more growth. But okay, for the sake of argument let’s suppose it also drops our per-capita GDP by 5%, from $53,000 to $50,300; that really doesn’t sound so bad, and any bigger drop than that is a totally unreasonable estimate based on prejudice rather than data. For the same tax rate might have to drop the basic income a bit too, say $6600 instead of $7000.

So, this is not a Pareto-improvement; we’re making some people better off, but others worse off. In fact, the way economists usually estimate Pareto-efficiency based on so-called “economic welfare”, they really just count up the total number of dollars and divide by the number of people and call it a day; so if we lose 5% in GDP they would register this as a Pareto-loss. (Yes, that’s a ridiculous way to do it for obvious reasons—$1 to Mitt Romney isn’t worth as much as it is to you and me—but it’s still how it’s usually done.)

But does that mean that it’s a bad idea? Not at all. In fact, if you assume that the real value—the utility—of a dollar decreases exponentially with each dollar you have, this policy could almost double the total happiness in US society. If you use a logarithm instead, it’s not quite as impressive; it’s only about a 20% improvement in total happiness—in other words, “only” making as much difference to the happiness of Americans from 2014 to 2015 as the entire period of economic growth from 1900 to 2000.

If right now you’re thinking, “Wow! Why aren’t we doing that?” that’s good, because I’ve been thinking the same thing for years. And maybe if we keep talking about it enough we can get people to start voting on it and actually make it happen.

But in order to make things like that happen, we must first get past the idea that Pareto-efficiency is the only thing that matters in moral decisions. And once again, that means overcoming the standard modes of thinking in neoclassical economics.

Something strange happened to economics in about 1950. Before that, economists from Marx to Smith to Keynes were always talking about differences in utility, marginal utility of wealth, how to maximize utility. But then economists stopped being comfortable talking about happiness, deciding (for reasons I still do not quite grasp) that it was “unscientific”, so they eschewed all discussion of the subject. Since we still needed to know why people choose what they do, a new framework was created revolving around “preferences”, which are a simple binary relation—you either prefer it or you don’t, you can’t like it “a lot more” or “a little more”—that is supposedly more measurable and therefore more “scientific”. But under this framework, there’s no way to say that giving a dollar to a homeless person makes a bigger difference to them than giving the same dollar to Mitt Romney, because a “bigger difference” is something you’ve defined out of existence. All you can say is that each would prefer to receive the dollar, and that both Mitt Romney and the homeless person would, given the choice, prefer to be Mitt Romney. While both of these things are true, it does seem to be kind of missing the point, doesn’t it?

There are stirrings of returning to actual talk about measuring actual (“cardinal”) utility, but still preferences (so-called “ordinal utility”) are the dominant framework. And in this framework, there’s really only one way to evaluate a situation as good or bad, and that’s Pareto-efficiency.

Actually, that’s not quite right; John Rawls cleverly came up with a way around this problem, by using the idea of “maximin”—maximize the minimum. Since each would prefer to be Romney, given the chance, we can say that the homeless person is worse off than Mitt Romney, and therefore say that it’s better to make the homeless person better off. We can’t say how much better, but at least we can say that it’s better, because we’re raising the floor instead of the ceiling. This is certainly a dramatic improvement, and on these grounds alone you can argue for the basic income—your floor is now explicitly set at the $6600 per year of the basic income.

But is that really all we can say? Think about how you make your own decisions; do you only speak in terms of strict preferences? I like Coke more than Pepsi; I like massages better than being stabbed. If preference theory is right, then there is no greater distance in the latter case than the former, because this whole notion of “distance” is unscientific. I guess we could expand the preference over groups of goods (baskets as they are generally called), and say that I prefer the set “drink Pepsi and get a massage” to the set “drink Coke and get stabbed”, which is certainly true. But do we really want to have to define that for every single possible combination of things that might happen to me? Suppose there are 1000 things that could happen to me at any given time, which is surely conservative. In that case there are 2^1000 = 10^300 possible combinations. If I were really just reading off a table of unrelated preference relations, there wouldn’t be room in my brain—or my planet—to store it, nor enough time in the history of the universe to read it. Even imposing rational constraints like transitivity doesn’t shrink the set anywhere near small enough—at best maybe now it’s 10^20, well done; now I theoretically could make one decision every billion years or so. At some point doesn’t it become a lot more parsimonious—dare I say, more scientific—to think that I am using some more organized measure than that? It certainly feels like I am; even if couldn’t exactly quantify it, I can definitely say that some differences in my happiness are large and others are small. The mild annoyance of drinking Pepsi instead of Coke will melt away in the massage, but no amount of Coke deliciousness is going to overcome the agony of being stabbed.

And indeed if you give people surveys and ask them how much they like things or how strongly they feel about things, they have no problem giving you answers out of 5 stars or on a scale from 1 to 10. Very few survey participants ever write in the comments box: “I was unable to take this survey because cardinal utility does not exist and I can only express binary preferences.” A few do write 1s and 10s on everything, but even those are fairly rare. This “cardinal utility” that supposedly doesn’t exist is the entire basis of the scoring system on Netflix and Amazon. In fact, if you use cardinal utility in voting, it is mathematically provable that you have the best possible voting system, which may have something to do with why Netflix and Amazon like it. (That’s another big “Why aren’t we doing this already?”)

If you can actually measure utility in this way, then there’s really not much reason to worry about Pareto-efficiency. If you just maximize utility, you’ll automatically get a Pareto-efficient result; but the converse is not true because there are plenty of Pareto-efficient scenarios that don’t maximize utility. Thinking back to our ultimatum game, all options are Pareto-efficient, but you can actually prove that the $5/$5 choice is the utility-maximizing one, if the two players have the same amount of wealth to start with. (Admittedly for those small amounts there isn’t much difference; but that’s also not too surprising, since $5 isn’t going to change anybody’s life.) And if they don’t—suppose I’m rich and you’re poor and we play the game—well, maybe I should give you more, precisely because we both know you need it more.

Perhaps even more significant, you can move from a Pareto-inefficient scenario to a Pareto-efficient one and make things worse in terms of utility. The scenario in which the top 1% are as wealthy as they can possibly be and the rest of us live on scraps may in fact be Pareto-efficient; but that doesn’t mean any of us should be interested in moving toward it (though sadly, we kind of are). If you’re only measuring in terms of Pareto-efficiency, your attempts at improvement can actually make things worse. It’s not that the concept is totally wrong; Pareto-efficiency is, other things equal, good; but other things are never equal.

So that’s Pareto-efficiency—and why you really shouldn’t care about it that much.