Month: March 2023

The role of innate activation in stochastic overload

PNRJ cognitive science, critique of neoclassical economics, heuristics and biases, mathematical models, personal , , , , , , , ,

Mar 26 JDN 2460030

Two posts ago I introduced my stochastic overload model, which offers an explanation for the Yerkes-Dodson effect by positing that additional stress increases sympathetic activation, which is useful up until the point where it starts risking an overload that forces systems to shut down and rest.

The central equation of the model is actually quite simple, expressed either as an expectation or as an integral:

Y = E[x + s | x + s < 1] P[x + s < 1]

Y = \int_{0}^{1-s} (x+s) dF(x)

The amount of output produced is the expected value of innate activation plus stress activation, times the probability that there is no overload. Increased stress raises this expectation value (the incentive effect), but also increases the probability of overload (the overload effect).

The model relies upon assuming that the brain starts with some innate level of activation that is partially random. Exactly what sort of Yerkes-Dodson curve you get from this model depends very much on what distribution this innate activation takes.

I’ve so far solved it for three types of distribution.

The simplest is a uniform distribution, where within a certain range, any level of activation is equally probable. The probability density function looks like this:

Assume the distribution has support between a and b, where a < b.

When b+s < 1, then overload is impossible, and only the incentive effect occurs; productivity increases linearly with stress.

The expected output is simply the expected value of a uniform distribution from a+s to b+s, which is:

E[x + s] = (a+b)/2+s

Then, once b+s > 1, overload risk begins to increase.

In this range, the probability of avoiding overload is:

P[x + s < 1] = F(1-s) = (1-s-a)/(b-a)

(Note that at b+s=1, this is exactly 1.)

The expected value of x+s in this range is:

E[x + s | x + s < 1] = (1-s)(1+s)/(2(b-a))

Multiplying these two together:

Y = [(1-s)(1+s)(1-s-a)]/[2(b-a)^2]

Here is what that looks like for a=0, b=1/2:

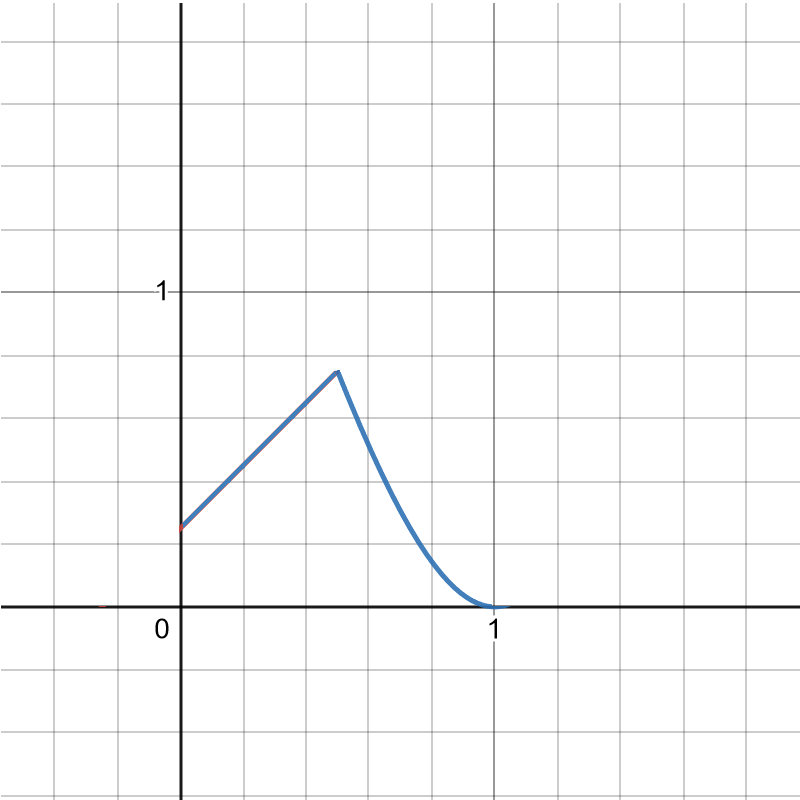
It does have the right qualitative features: increasing, then decreasing. But its sure looks weird, doesn’t it? It has this strange kinked shape.

So let’s consider some other distributions.

The next one I was able to solve it for is an exponential distribution, where the most probable activation is zero, and then higher activation always has lower probability than lower activation in an exponential decay:

For this it was actually easiest to do the integral directly (I did it by integrating by parts, but I’m sure you don’t care about all the mathematical steps):

Y = \int_{0}^{1-s} (x+s) dF(x)

Y = (1/λ+s) – (1/ λ + 1)e^(-λ(1-s))

The parameter λdecides how steeply your activation probability decays. Someone with low λ is relatively highly activated all the time, while someone with high λ is usually not highly activated; this seems like it might be related to the personality trait neuroticism.

Here are graphs of what the resulting Yerkes-Dodson curve looks like for several different values of λ:

λ = 0.5:

λ = 1:

λ = 2:

λ = 4:

λ = 8:

The λ = 0.5 person has high activation a lot of the time. They are actually fairly productive even without stress, but stress quickly overwhelms them. The λ = 8 person has low activation most of the time. They are not very productive without stress, but can also bear relatively high amounts of stress without overloading.

(The low-λ people also have overall lower peak productivity in this model, but that might not be true in reality, if λ is inversely correlated with some other attributes that are related to productivity.)

Neither uniform nor exponential has the nice bell-curve shape for innate activation we might have hoped for. There is another class of distributions, beta distributions, which do have this shape, and they are sort of tractable—you need something called an incomplete beta function, which isn’t an elementary function but it’s useful enough that most statistical packages include it.

Beta distributions have two parameters, α and β. They look like this:

Beta distributions are quite useful in Bayesian statistics; if you’re trying to estimate the probability of a random event that either succeeds or fails with a fixed probability (a Bernoulli process), and so far you have observed a successes and b failures, your best guess of its probability at each trial is a beta distribution with α = a+1 and β = b+1.

For beta distributions with parameters α and β, the result comes out to (I is that incomplete beta function I mentioned earlier):

Y = I(1-s, α+1, β) + I(1-s, α, β)

For whole number values of α andβ, the incomplete beta function can be computed by hand (though it is more work the larger they are); here’s an example with α = β = 2.

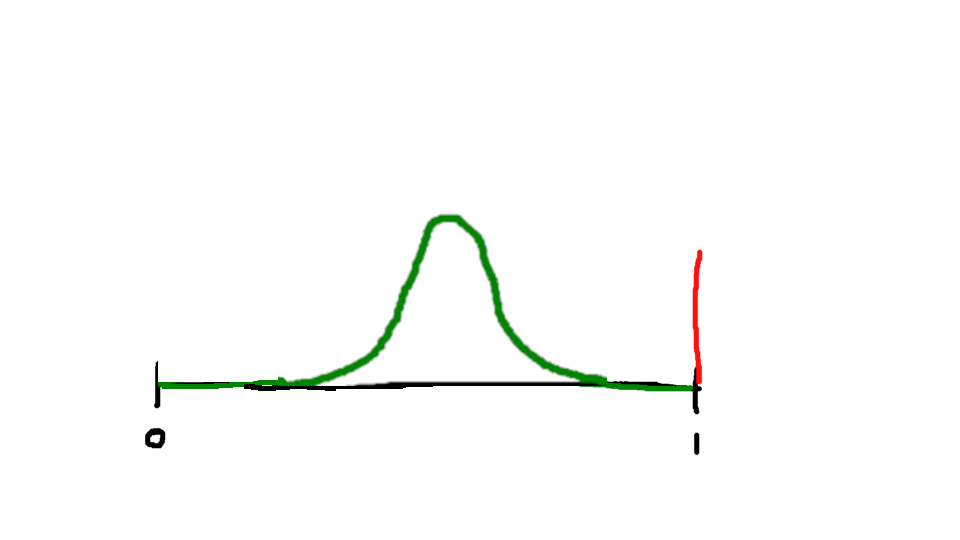
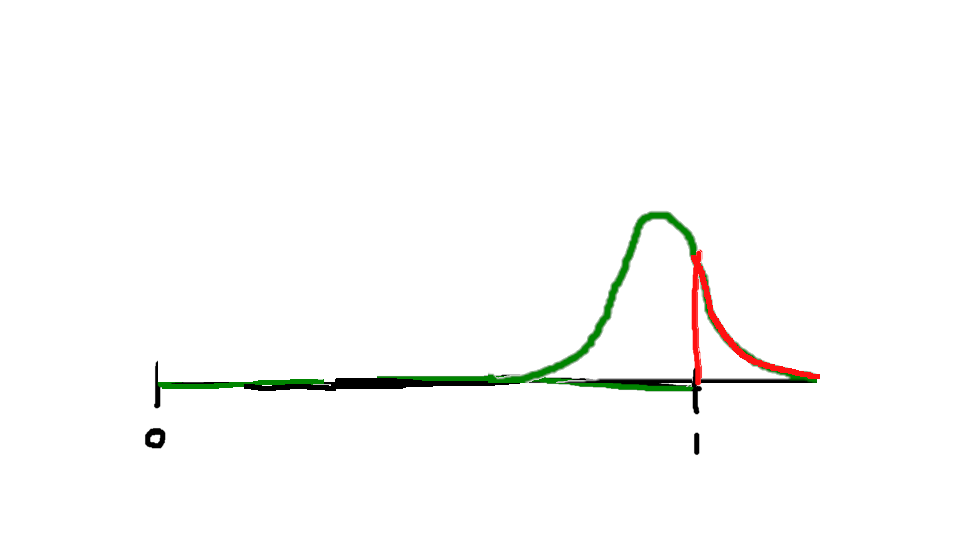
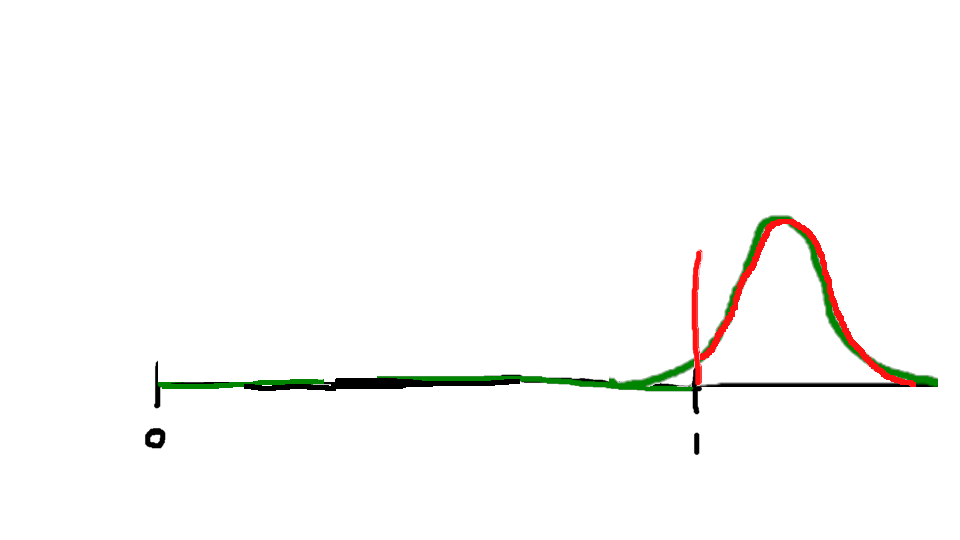
The innate activation probability looks like this:

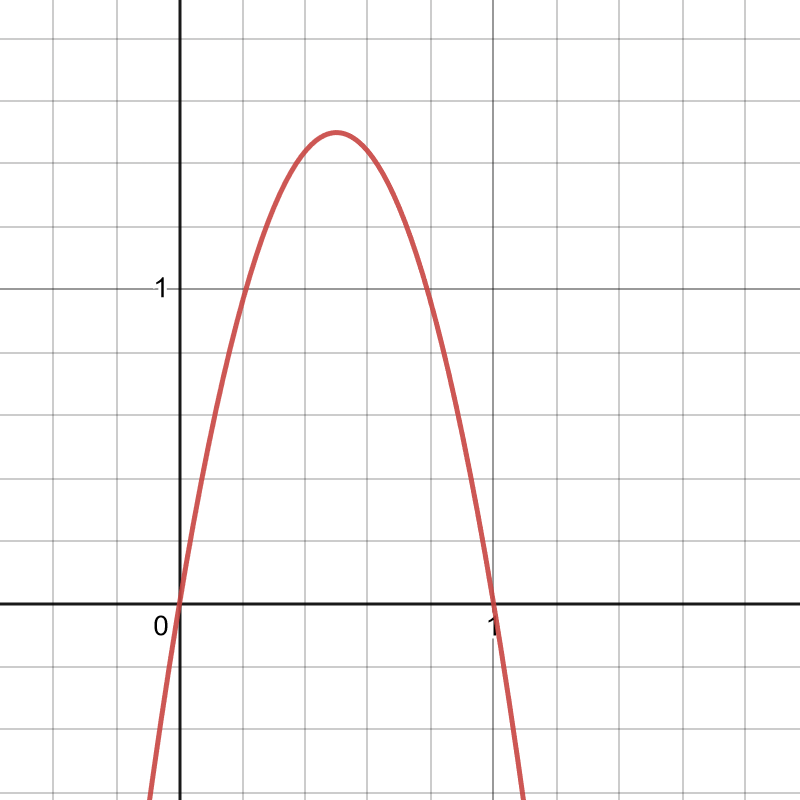
And the result comes out like this:

Y = 2(1-s)^3 – 3/2(1-s)^4 + 3s(1-s)^2 – 2s(1-s)^3

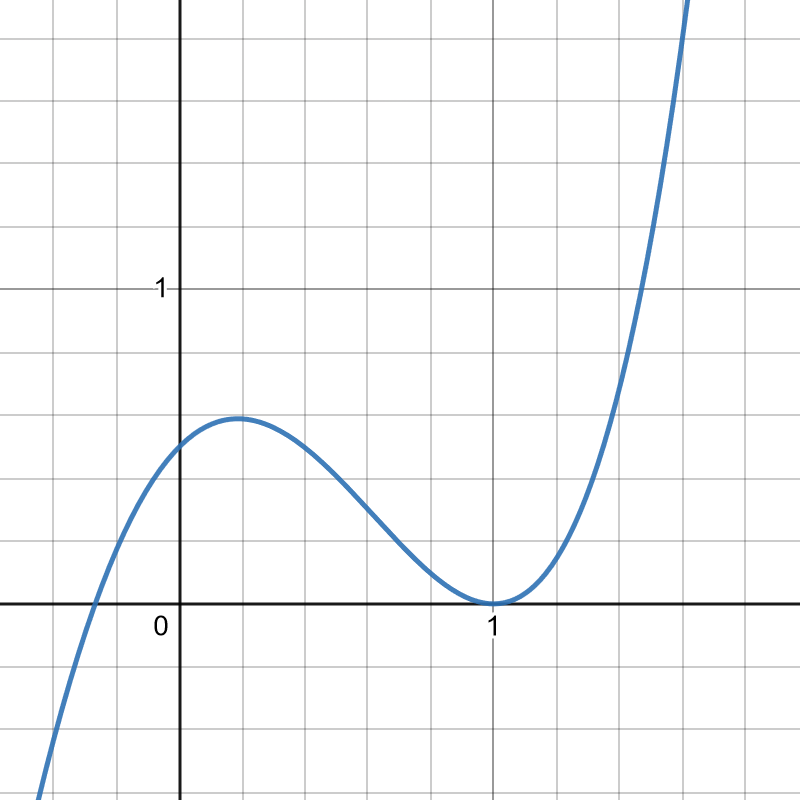
This person has pretty high innate activation most of the time, so stress very quickly overwhelms them. If I had chosen a much higher β, I could change that, making them less likely to be innately so activated.

These are the cases I’ve found to be relatively tractable so far. They all have the right qualitative pattern: Increasing stress increases productivity for awhile, then begins decreasing it once overload risk becomes too high. They also show a general pattern where people who are innately highly activated (neurotic?) are much more likely to overload and thus much more sensitive to stress.

What happens when a bank fails

PNRJ critique of neoclassical economics, current events, inequality, macroeconomics, market failure, public policy , , , , , , , , , , , , , , , ,

Mar 19 JDN 2460023

As of March 9, Silicon Valley Bank (SVB) has failed and officially been put into receivership under the FDIC. A bank that held $209 billion in assets has suddenly become insolvent.

This is the second-largest bank failure in US history, after Washington Mutual (WaMu) in 2008. In fact it will probably have more serious consequences than WaMu, for two reasons:

1. WaMu collapsed as part of the Great Recession, so there was already a lot of other things going on and a lot of policy responses already in place.

2. WaMu was mostly a conventional commercial bank that held deposits and loans for consumers, so its assets were largely protected by the FDIC, and thus its bankruptcy didn’t cause contagion the spread out to the rest of the system. (Other banks—shadow banks—did during the crash, but not so much WaMu.) SVB mostly served tech startups, so a whopping 89% of its deposits were not protected by FDIC insurance.

You’ve likely heard of many of the companies that had accounts at SVB: Roku, Roblox, Vimeo, even Vox. Stocks of the US financial industry lost $100 billion in value in two days.

The good news is that this will not be catastrophic. It probably won’t even trigger a recession (though the high interest rates we’ve been having lately potentially could drive us over that edge). Because this is commercial banking, it’s done out in the open, with transparency and reasonably good regulation. The FDIC knows what they are doing, and even though they aren’t covering all those deposits directly, they intend to find a buyer for the bank who will, and odds are good that they’ll be able to cover at least 80% of the lost funds.

In fact, while this one is exceptionally large, bank failures are not really all that uncommon. There have been nearly 100 failures of banks with assets over $1 billion in the US alone just since the 1970s. The FDIC exists to handle bank failures, and generally does the job well.

Then again, it’s worth asking whether we should really have a banking system in which failures are so routine.

The reason banks fail is kind of a dark open secret: They don’t actually have enough money to cover their deposits.

Banks loan away most of their cash, and rely upon the fact that most of their depositors will not want to withdraw their money at the same time. They are required to keep a certain ratio in reserves, but it’s usually fairly small, like 10%. This is called fractional-reserve banking.

As long as less than 10% of deposits get withdrawn at any given time, this works. But if a bunch of depositors suddenly decide to take out their money, the bank may not have enough to cover it all, and suddenly become insolvent.

In fact, the fear that a bank might become insolvent can actually cause it to become insolvent, in a self-fulfilling prophecy. Once depositors get word that the bank is about to fail, they rush to be the first to get their money out before it disappears. This is a bank run, and it’s basically what happened to SVB.

The FDIC was originally created to prevent or mitigate bank runs. Not only did they provide insurance that reduced the damage in the event of a bank failure; by assuring depositors that their money would be recovered even if the bank failed, they also reduced the chances of a bank run becoming a self-fulfilling prophecy.


Indeed, SVB is the exception that proves the rule, as they failed largely because their assets were mainly not FDIC insured.

Fractional-reserve banking effectively allows banks to create money, in the form of credit that they offer to borrowers. That credit gets deposited in other banks, which then go on to loan it out to still others; the result is that there is more money in the system than was ever actually printed by the central bank.

In most economies this commercial bank money is a far larger quantity than the central bank money actually printed by the central bank—often nearly 10 to 1. This ratio is called the money multiplier.

Indeed, it’s not a coincidence that the reserve ratio is 10% and the multiplier is 10; the theoretical maximum multiplier is always the inverse of the reserve ratio, so if you require reserves of 10%, the highest multiplier you can get is 10. Had we required 20% reserves, the multiplier would drop to 5.

Most countries have fractional-reserve banking, and have for centuries; but it’s actually a pretty weird system if you think about it.

Back when we were on the gold standard, fractional-reserve banking was a way of cheating, getting our money supply to be larger than the supply of gold would actually allow.

But now that we are on a pure fiat money system, it’s worth asking what fractional-reserve banking actually accomplishes. If we need more money, the central bank could just print more. Why do we delegate that task to commercial banks?

David Friedman of the Cato Institute had some especially harsh words on this, but honestly I find them hard to disagree with:

Before leaving the subject of fractional reserve systems, I should mention one particularly bizarre variant — a fractional reserve system based on fiat money. I call it bizarre because the essential function of a fractional reserve system is to reduce the resource cost of producing money, by allowing an ounce of reserves to replace, say, five ounces of currency. The resource cost of producing fiat money is zero; more precisely, it costs no more to print a five-dollar bill than a one-dollar bill, so the cost of having a larger number of dollars in circulation is zero. The cost of having more bills in circulation is not zero but small. A fractional reserve system based on fiat money thus economizes on the cost of producing something that costs nothing to produce; it adds the disadvantages of a fractional reserve system to the disadvantages of a fiat system without adding any corresponding advantages. It makes sense only as a discreet way of transferring some of the income that the government receives from producing money to the banking system, and is worth mentioning at all only because it is the system presently in use in this country.

Our banking system evolved gradually over time, and seems to have held onto many features that made more sense in an earlier era. Back when we had arbitrarily tied our central bank money supply to gold, creating a new money supply that was larger may have been a reasonable solution. But today, it just seems to be handing the reins over to private corporations, giving them more profits while forcing the rest of society to bear more risk.

The obvious alternative is full-reserve banking, where banks are simply required to hold 100% of their deposits in reserve and the multiplier drops to 1. This idea has been supported by a number of quite prominent economists, including Milton Friedman.

It’s not just a right-wing idea: The left-wing organization Positive Money is dedicated to advocating for a full-reserve banking system in the UK and EU. (The ECB VP’s criticism of the proposal is utterly baffling to me: it “would not create enough funding for investment and growth.” Um, you do know you can print more money, right? Hm, come to think of it, maybe the ECB doesn’t know that, because they think inflation is literally Hitler. There are legitimate criticisms to be had of Positive Money’s proposal, but “There won’t be enough money under this fiat money system” is a really weird take.)

There’s a relatively simple way to gradually transition from our current system to a full-reserve sytem: Simply increase the reserve ratio over time, and print more central bank money to keep the total money supply constant. If we find that it seems to be causing more problems than it solves, we could stop or reverse the trend.

Krugman has pointed out that this wouldn’t really fix the problems in the banking system, which actually seem to be much worse in the shadow banking sector than in conventional commercial banking. This is clearly right, but it isn’t really an argument against trying to improve conventional banking. I guess if stricter regulations on conventional banking push more money into the shadow banking system, that’s bad; but really that just means we should be imposing stricter regulations on the shadow banking system first (or simultaneously).

We don’t need to accept bank runs as a routine part of the financial system. There are other ways of doing things.

The stochastic overload model

PNRJ cognitive science, mathematical models, personal, science and academia , , , , , , , ,

The stochastic overload model

Mar 12 JDN 2460016

The next few posts are going to be a bit different, a bit more advanced and technical than usual. This is because, for the first time in several months at least, I am actually working on what could be reasonably considered something like theoretical research.

I am writing it up in the form of blog posts, because actually writing a paper is still too stressful for me right now. This also forces me to articulate my ideas in a clearer and more readable way, rather than dive directly into a morass of equations. It also means that even if I do never actually get around to finishing a paper, the idea is out there, and maybe someone else could make use of it (and hopefully give me some of the credit).

I’ve written previously about the Yerkes-Dodson effect: On cognitively-demanding tasks, increased stress increases performance, but only to a point, after which it begins decreasing it again. The effect is well-documented, but the mechanism is poorly understood.

I am currently on the wrong side of the Yerkes-Dodson curve, which is why I’m too stressed to write this as a formal paper right now. But that also gave me some ideas about how it may work.

I have come up with a simple but powerful mathematical model that may provide a mechanism for the Yerkes-Dodson effect.

This model is clearly well within the realm of a behavioral economic model, but it is also closely tied to neuroscience and cognitive science.

I call it the stochastic overload model.

First, a metaphor: Consider an engine, which can run faster or slower. If you increase its RPMs, it will output more power, and provide more torque—but only up to a certain point. Eventually it hits a threshold where it will break down, or even break apart. In real engines, we often include safety systems that force the engine to shut down as it approaches such a threshold.

I believe that human brains function on a similar principle. Stress increases arousal, which activates a variety of processes via the sympathetic nervous system. This activation improves performance on both physical and cognitive tasks. But it has a downside; especially on cognitively demanding tasks which required sustained effort, I hypothesize that too much sympathetic activation can result in a kind of system overload, where your brain can no longer handle the stress and processes are forced to shut down.

This shutdown could be brief—a few seconds, or even a fraction of a second—or it could be prolonged—hours or days. That might depend on just how severe the stress is, or how much of your brain it requires, or how prolonged it is. For purposes of the model, this isn’t vital. It’s probably easiest to imagine it being a relatively brief, localized shutdown of a particular neural pathway. Then, your performance in a task is summed up over many such pathways over a longer period of time, and by the law of large numbers your overall performance is essentially the average performance of all your brain systems.

That’s the “overload” part of the model. Now for the “stochastic” part.

Let’s say that, in the absence of stress, your brain has a certain innate level of sympathetic activation, which varies over time in an essentially chaotic, unpredictable—stochastic—sort of way. It is never really completely deactivated, and may even have some chance of randomly overloading itself even without outside input. (Actually, a potential role in the model for the personality trait neuroticism is an innate tendency toward higher levels of sympathetic activation in the absence of outside stress.)

Let’s say that this innate activation is x, which follows some kind of known random distribution F(x).

For simplicity, let’s also say that added stress s adds linearly to your level of sympathetic activation, so your overall level of activation is x + s.

For simplicity, let’s say that activation ranges between 0 and 1, where 0 is no activation at all and 1 is the maximum possible activation and triggers overload.

I’m assuming that if a pathway shuts down from overload, it doesn’t contribute at all to performance on the task. (You can assume it’s only reduced performance, but this adds complexity without any qualitative change.)

Since sympathetic activation improves performance, but can result in overload, your overall expected performance in a given task can be computed as the product of two terms:

[expected value of x + s, provided overload does not occur] * [probability overload does not occur]

E[x + s | x + s < 1] P[x + s < 1]

The first term can be thought of as the incentive effect: Higher stress promotes more activation and thus better performance.

The second term can be thought of as the overload effect: Higher stress also increases the risk that activation will exceed the threshold and force shutdown.

This equation actually turns out to have a remarkably elegant form as an integral (and here’s where I get especially technical and mathematical):

\int_{0}^{1-s} (x+s) dF(x)

The integral subsumes both the incentive effect and the overload effect into one term; you can also think of the +s in the integrand as the incentive effect and the 1-s in the limit of integration as the overload effect.

For the uninitated, this is probably just Greek. So let me show you some pictures to help with your intuition. These are all freehand sketches, so let me apologize in advance for my limited drawing skills. Think of this as like Arthur Laffer’s famous cocktail napkin.

Suppose that, in the absence of outside stress, your innate activation follows a distribution like this (this could be a normal or logit PDF; as I’ll talk about next week, logit is far more tractable):

As I start adding stress, this shifts the distribution upward, toward increased activation:

Initially, this will improve average performance.

But at some point, increased stress actually becomes harmful, as it increases the probability of overload.

And eventually, the probability of overload becomes so high that performance becomes worse than it was with no stress at all:

The result is that overall performance, as a function of stress, looks like an inverted U-shaped curve—the Yerkes-Dodson curve:

The precise shape of this curve depends on the distribution that we use for the innate activation, which I will save for next week’s post.

Mental accounting and “free shipping”

PNRJ financial advice, heuristics and biases , , ,

Mar 5 JDN 2460009

Suppose you are considering buying a small item, such as a hardcover book or a piece of cookware. If you buy it from one seller, the price is $50, but shipping costs $20; if you buy it from another, it costs $70 but you’ll get free shipping. Which one do you buy from?

If you are being rational, you won’t care in the slightest. But most people don’t seem to behave that way. The idea of paying $20 to ship a $50 item just feels wrong somehow, and so most people will tend to prefer the seller with free shipping—even though the total amount they spend is the same.

Sellers know this, and take advantage of it. Indeed, it is the only plausible reason they would ever offer free shipping in the first place.

Free shipping, after all, is not actually free. Someone still gets paid to perform that delivery. And while the seller is the one making the payment, they will no doubt raise the price they charge you as a customer in order to make up the difference—it would be very foolish of them not to. So ultimately, everything turns out the same as if you had paid for shipping.

But it still feels different, doesn’t it? This is because of a series of heuristics most people use for their financial decisions known as mental accounting.

There are a lot of different heuristics that go into mental accounting, but the one that is most relevant here is mental budgeting: We divide our spending into different budgetary categories, and try not to go over budget in any particular category.

While the item you’re buying may in fact be worth more than $70 to you, you probably didn’t budget in your mind $20 for shipping. So even if the total impact on your finances is the same, you register the higher shipping price as “over budget” in one of your mental categories. So it feels like you are spending more than if you had simply paid $70 for the item and gotten free shipping. Even though you are actually paying exactly the same amount.

Another reason this works so well may be that people don’t really have a clear idea what the price of items is at different sellers. So you see “$70, free shipping” and you assume that it previously had a price of $70 and they are generously offering you shipping for free.

But if you ever find yourself assuming that a corporation is being generous—you are making a cognitive error. Corporations are, by design, as selfish as possible. They are never generous. There is always something in it for them.

In the best-case scenario, what serves the company will also serve other people, as when they donate to good causes for tax deductions and better PR (or when they simply provide good products at low prices). But no corporation is going to intentionally sacrifice its own interests to benefit anyone else. They exist to maximize profits for their shareholders. That is what they do. That is what they always do. Keep that in mind, and you won’t be disappointed by them.

They might offer you a lower price, or other perks, in order to keep you as a customer; but they will do so very carefully, only enough to keep you from shopping elsewhere. And if they are able to come down on the price while still making a profit, that really just goes to show they had too much market power to begin with.

Free shipping, at least, is relatively harmless. It’s slightly manipulative, but a higher price plus free shipping really does ultimately amount to the same thing as a lower price plus paid shipping. The worst I can say about it is that it may cause people to buy things they otherwise wouldn’t have; but they must have still felt that the sticker price was worth it, so it can’t really be so bad.

Another, more sinister way that corporations use mental accounting to manipulate customers is through the use of credit cards.

It’s well-documented that people are willing to spend more on credit cards than they would be in cash. In most cases, this does not appear to be the result of people actually being constrained by their liquidity—even if people have the cash, they are more willing to spend a credit card to buy the same item.

This effect is called pain of paying. It hurts more, psychologically, to hand over a series of dollar bills than it does to swipe (or lately, just tap) a credit card. It’s not just about convenience; by making it less painful to pay, companies can pressure us to spend more.

And since credit cards add to an existing balance, there is what’s called transaction decoupling: The money we spent on any particular item gets mentally separated from the actual transaction in which we bought that item. We may not even remember how much we paid. We just see a credit card balance go up; and it may end up being quite a large balance, but any particular transaction usually won’t have raised it very much.

Human beings tend to perceive stimuli proportionally: We don’t really feel the effect of $5 per se, we feel the effect of a 20% increase. So that $5 feels like a lot more when it’s coming out of a wallet that held $20 than it does when it’s adding to a $200 credit card balance.

This is also why I say expensive cheap things, cheap expensive things; you should care more about the same proportional difference when it’s on a higher base price.