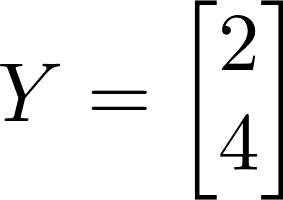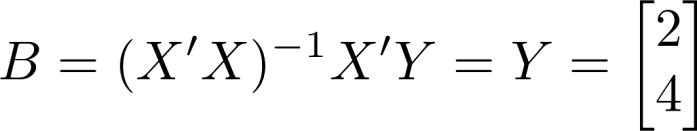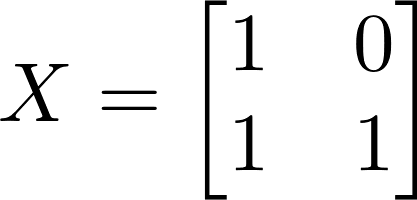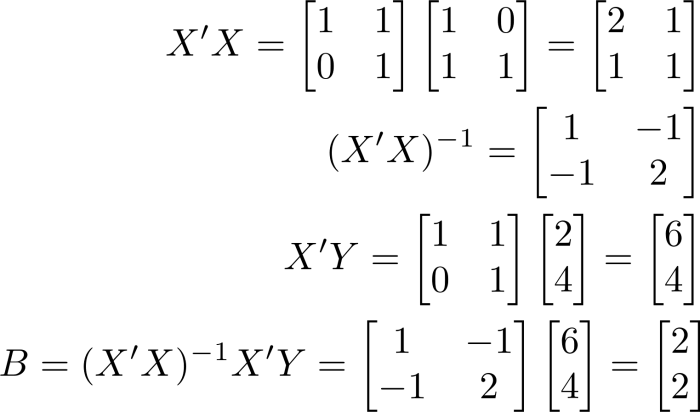Month: November 2017

What exactly is “gentrification”? How should we deal with it?

PNRJ development economics, ethics, inequality, market failure, public policy , , , , , , , , , , , , ,

Nov 26, JDN 2458083

“Gentrification” is a word that is used in a variety of mutually-inconsistent ways. If you compare the way social scientists use it to the way journalists use it, for example, they are almost completely orthogonal.

The word “gentrification” is meant to invoke the concept of a feudal gentry—a hereditary landed class that extracts rents from the rest of the population while contributing little or nothing themselves.

If indeed that is what we are talking about, then obviously this is bad. Moreover, it’s not an entirely unfounded fear; there are some remarkably strong vestiges of feudalism in the developed world, even in the United States where we never formally had a tradition of feudal titles. There really is a significant portion of the world’s wealth held by a handful of billionaire landowner families.

But usually when people say “gentrification” they mean something much broader. Almost any kind of increase in urban real estate prices gets characterized as “gentrification” by at least somebody, and herein lies the problem.

In fact, the kind of change that is most likely to get characterized as “gentrification” isn’t even the rising real estate prices we should be most worried about. People aren’t concerned when the prices of suburban homes double in 20 years. You might think that things that are already too expensive getting more expensive would be the main concern, but on the contrary, people are most likely to cry “gentrification” when housing prices rise in poor areas where housing is cheap.

One of the most common fears about gentrification is that it will displace local residents. In fact, the best quasi-experimental studies show little or no displacement effect. It’s actually mainly middle-class urbanites who get displaced by rising rents. Poor people typically own their homes, and actually benefit from rising housing prices. Young upwardly-mobile middle-class people move to cities to rent apartments near where they work, and tend to assume that’s how everyone lives, but it’s not. Rising rents in a city are far more likely to push out its grad students than they are poor families that have lived there for generations. Part of why displacement does not occur may be because of policies specifically implemented to fight it, such as subsidized housing and rent control. If that’s so, let’s keep on subsidizing housing (though rent control will always be a bad idea).

Nor is gentrification actually a very widespread phenomenon. The majority of poor neighborhoods remain poor indefinitely. In most studies, only about 30% of neighborhoods classified as “gentrifiable” actually end up “gentrifying”. Less than 10% of the neighborhoods that had high poverty rates in 1970 had low poverty rates in 2010.

Most people think gentrification reduces crime, but in the short run the opposite is the case. Robbery and larceny are higher in gentrifying neighborhoods. Criminals are already there, and suddenly they get much more valuable targets to steal from, so they do.

There is also a general perception that gentrification involves White people pushing Black people out, but this is also an overly simplistic view. First of all, a lot of gentrification is led by upwardly-mobile Black and Latino people. Black people who live in gentrified neighborhoods seem to be better off than Black people who live in non-gentrified neighborhoods; though selection bias may contribute to this effect, it can’t be all that strong, or we’d observe a much stronger displacement effect. Moreover, some studies have found that gentrification actually tends to increase the racial diversity of neighborhoods, and may actually help fight urban self-segregation, though it does also tend to increase racial polarization by forcing racial mixing.

What should we conclude from all this? I think the right conclusion is we are asking the wrong question.

Rising housing prices in poor areas aren’t inherently good or inherently bad, and policies designed specifically to increase or decrease housing prices are likely to have harmful side effects. What we need to be focusing on is not houses or neighborhoods but people. Poverty is definitely a problem, for sure. Therefore we should be fighting poverty, not “gentrification”. Directly transfer wealth from the rich to the poor, and then let the housing market fall where it may.

There is still some role for government in urban planning more generally, regarding things like disaster preparedness, infrastructure development, and transit systems. It may even be worthwhile to design regulations or incentives that directly combat racial segregation at the neighborhood level, for, as the Schelling Segregation Model shows, it doesn’t take a large amount of discriminatory preference to have a large impact on socioeconomic outcomes. But don’t waste effort fighting “gentrification”; directly design policies that will incentivize desegregation.

Rising rent as a proportion of housing prices is still bad, and the fundamental distortions in our mortgage system that prevent people from buying houses are a huge problem. But rising housing prices are most likely to be harmful in rich neighborhoods, where housing is already overpriced; in poor neighborhoods where housing is cheap, rising prices might well be a good thing.
In fact, I have a proposal to rapidly raise homeownership across the United States, which is almost guaranteed to work, directly corrects an enormous distortion in financial markets, and would cost about as much as the mortgage interest deduction (which should probably be eliminated, as most economists agree). Give each US adult a one-time grant voucher which gives them $40,000 that can only be spent as a down payment on purchasing a home. Each time someone turns 18, they get a voucher. You only get one over your lifetime, so use it wisely (otherwise the policy could become extremely expensive); but this is an immediate direct transfer of wealth that also reduces your credit constraint. I know I for one would be house-hunting right now if I were offered such a voucher. The mortgage interest deduction means nothing to me, because I can’t afford a down payment. Where the mortgage interest deduction is regressive, benefiting the rich more than the poor, this policy gives everyone the same amount, like a basic income.

In the short run, this policy would probably be expensive, as we’d have to pay out a large number of vouchers at once; but with our current long-run demographic trends, the amortized cost is basically the same as the mortgage interest deduction. And the US government especially should care about the long-run amortized cost, as it is an institution that has lasted over 200 years without ever missing a payment and can currently borrow at negative real interest rates.

Why risking nuclear war should be a war crime

PNRJ ethics, public policy , , , , , , , , , ,

Nov 19, JDN 2458078

“What is the value of a human life?” is a notoriously difficult question, probably because people keep trying to answer it in terms of dollars, and it rightfully offends our moral sensibilities to do so. We shouldn’t be valuing people in terms of dollars—we should be valuing dollars in terms of their benefits to people.

So let me ask a simpler question: Does the value of an individual human life increase, decrease, or stay the same, as we increase the number of people in the world?

A case can be made that it should stay the same: Why should my value as a person depend upon how many other people there are? Everything that I am, I still am, whether there are a billion other people or a thousand.

But in fact I think the correct answer is that it decreases. This is for two reasons: First, anything that I can do is less valuable if there are other people who can do it better. This is true whether we’re talking about writing blog posts or ending world hunger. Second, and most importantly, if the number of humans in the world gets small enough, we begin to face danger of total permanent extinction.

If the value of a human life is constant, then 1,000 deaths is equally bad whether it happens in a population of 10,000 or a population of 10 billion. That doesn’t seem right, does it? It seems more reasonable to say that losing ten percent should have a roughly constant effect; in that case losing 1,000 people in a population of 10,000 is equally bad as losing 1 billion in a population of 10 billion. If that seems too strong, we could choose some value in between, and say perhaps that losing 1,000 out of 10,000 is equally bad as losing 1 million out of 1 billion. This would mean that the value of 1 person’s life today is about 1/1,000 of what it was immediately after the Toba Event.

Of course, with such uncertainty, perhaps it’s safest to assume constant value. This seems the fairest, and it is certainly a reasonable approximation.

In any case, I think it should be obvious that the inherent value of a human life does not increase as you add more human lives. Losing 1,000 people out of a population of 7 billion is not worse than losing 1,000 people out of a population of 10,000. That way lies nonsense.

Yet if we agree that the value of a human life is not increasing, this has a very important counter-intuitive consequence: It means that increasing the risk of a global catastrophe is at least as bad as causing a proportional number of deaths. Specifically, it implies that a 1% risk of global nuclear war is worse than killing 10 million people outright.

The calculation is simple: If the value of a human life is a constant V, then the expected utility (admittedly, expected utility theory has its flaws) from killing 10 million people is -10 million V. But the expected utility from a 1% risk of global nuclear war is 1% times -V times the expected number of deaths from such a nuclear war—and I think even 2 billion is a conservative estimate. (0.01)(-2 billion) V = -20 million V.

This probably sounds too abstract, or even cold, so let me put it another way. Suppose we had the choice between two worlds, and these were the only worlds we could choose from. In world A, there are 100 leaders who each make choices that result in 10 million deaths. In world B, there are 100 leaders who each make choices that result in a 1% chance of nuclear war. Which world should we choose?

The choice is a terrible one, to be sure.

In world A, 1 billion people die.

Yet what happens in world B?

If the risks are independent, we can’t just multiply by 100 to get a guarantee of nuclear war. The actual probability is 1-(1-0.01)^100 = 63%. Yet even so, (0.63)(2 billion) = 1.26 billion. The expected number of deaths is higher in world B. Indeed, the most likely scenario is that 2 billion people die.

Yet this is probably too conservative. The risks are most likely positively correlated; two world leaders who each take a 1% chance of nuclear war probably do so in response to one another. Therefore maybe adding up the chances isn’t actually so unreasonable—for all practical intents and purposes, we may be best off considering nuclear war in world B as guaranteed to happen. In that case, world B is even worse.

And that is all assuming that the nuclear war is relatively contained. Major cities are hit, then a peace treaty is signed, and we manage to rebuild human civilization more or less as it was. This is what most experts on the issue believe would happen; but I for one am not so sure. The nuclear winter and total collapse of institutions and infrastructure could result in a global apocalypse that would result in human extinction—not 2 billion deaths but 7 billion, and an end to all of humanity’s projects once and forever This is the kind of outcome we should be prepared to do almost anything to prevent.

What does this imply for global policy? It means that we should be far more aggressive in punishing any action that seems to bring the world closer to nuclear war. Even tiny increases in risk, of the sort that would ordinarily be considered negligible, are as bad as murder. A measurably large increase is as bad as genocide.

Of course, in practice, we have to be able to measure something in order to punish it. We can’t have politicians imprisoned over 0.000001% chances of nuclear war, because such a chance is so tiny that there would be no way to attain even reasonable certainty that such a change had even occurred, much less who was responsible.

Even for very large chances—and in this context, 1% is very large—it would be highly problematic to directly penalize increasing the probability, as we have no consistent, fair, objective measure of that probability.

Therefore in practice what I think we must do is severely and mercilessly penalize certain types of actions that would be reasonably expected to increase the probability of catastrophic nuclear war.

If we had the chance to start over from the Manhattan Project, maybe simply building a nuclear weapon should be considered a war crime. But at this point, nuclear proliferation has already proceeded far enough that this is no longer a viable option. At least the US and Russia for the time being seem poised to maintain their nuclear arsenals, and in fact it’s probably better for them to keep maintaining and updating them rather than leaving decades-old ICBMs to rot.

What can we do instead?

First, we probably need to penalize speech that would tend to incite war between nuclear powers. Normally I am fiercely opposed to restrictions on speech, but this is nuclear war we’re talking about. We can’t take any chances on this one. If there is even a slight chance that a leader’s rhetoric might trigger a nuclear conflict, they should be censored, punished, and probably even imprisoned. Making even a veiled threat of nuclear war is like pointing a gun at someone’s head and threatening to shoot them—only the gun is pointed at everyone’s head simultaneously. This isn’t just yelling “fire” in a crowded theater; it’s literally threatening to burn down every theater in the world at once.

Such a regulation must be designed to allow speech that is necessary for diplomatic negotiations, as conflicts will invariably arise between any two countries. We need to find a way to draw the line so that it’s possible for a US President to criticize Russia’s intervention in the Ukraine or for a Chinese President to challenge US trade policy, without being accused of inciting war between nuclear powers. But one thing is quite clear: Wherever we draw that line, President Trump’s statement about “fire and fury” definitely crosses it. This is a direct threat of nuclear war, and it should be considered a war crime. That reason by itself—let alone his web of Russian entanglements and violations of the Emoluments Clause—should be sufficient to not only have Trump removed from office, but to have him tried at the Hague. Impulsiveness and incompetence are no excuse when weapons of mass destruction are involved.

Second, any nuclear policy that would tend to increase first-strike capability rather than second-strike capability should be considered a violation of international law. In case you are unfamiliar with such terms: First-strike capability consists of weapons such as ICBMs that are only viable to use as the opening salvo of an attack, because their launch sites can be easily located and targeted. Second-strike capability consists of weapons such as submarines that are more concealable, so it’s much more likely that they could wait for an attack to happen, confirm who was responsible and how much damage was done, and then retaliate afterward.
Even that retaliation would be difficult to justify: It’s effectively answering genocide with genocide, the ultimate expression of “an eye for an eye” writ large upon humanity’s future. I’ve previously written about my Credible Targeted Conventional Response strategy that makes it both more ethical and more credible to respond to a nuclear attack with a non-nuclear retaliation. But at least second-strike weapons are not inherently only functional at starting a nuclear war. A first-strike weapon can theoretically be fired in response to a surprise attack, but only before the attack hits you—which gives you literally minutes to decide the fate of the world, most likely with only the sketchiest of information upon which to base your decision. Second-strike weapons allow deliberation. They give us a chance to think carefully for a moment before we unleash irrevocable devastation.

All the launch codes should of course be randomized onetime pads for utmost security. But in addition to the launch codes themselves, I believe that anyone who wants to launch a nuclear weapon should be required to type, letter by letter (no copy-pasting), and then have the machine read aloud, Oppenheimer’s line about Shiva, “Now I am become Death, the destroyer of worlds.” Perhaps the passphrase should conclude with something like “I hereby sentence millions of innocent children to death by fire, and millions more to death by cancer.” I want it to be as salient as possible in the heads of every single soldier and technician just exactly how many innocent people they are killing. And if that means they won’t turn the key—so be it. (Indeed, I wouldn’t mind if every Hellfire missile required a passphrase of “By the authority vested in me by the United States of America, I hereby sentence you to death or dismemberment.” Somehow I think our drone strike numbers might go down. And don’t tell me they couldn’t; this isn’t like shooting a rifle in a firefight. These strikes are planned days in advance and specifically designed to be unpredictable by their targets.)

If everyone is going to have guns pointed at each other, at least in a second-strike world they’re wearing body armor and the first one to pull the trigger won’t automatically be the last one left standing.

Third, nuclear non-proliferation treaties need to be strengthened into disarmament treaties, with rapid but achievable timelines for disarmament of all nuclear weapons, starting with the nations that have the largest arsenals. Random inspections of the disarmament should be performed without warning on a frequent schedule. Any nation that is so much as a day late on their disarmament deadlines needs to have its leaders likewise hauled off to the Hague. If there is any doubt at all in your mind whether your government will meet its deadlines, you need to double your disarmament budget. And if your government is too corrupt or too bureaucratic to meet its deadlines even if they try, well, you’d better shape up fast. We’ll keep removing and imprisoning your leaders until you do. Once again, nothing can be left to chance.

We might want to maintain some small nuclear arsenal for the sole purpose of deflecting asteroids from colliding with the Earth. If so, that arsenal should be jointly owned and frequently inspected by both the United States and Russia—not just the nuclear superpowers, but also the only two nations with sufficient rocket launch capability in any case. The launch of the deflection missiles should require joint authorization from the presidents of both nations. But in fact nuclear weapons are probably not necessary for such a deflection; nuclear rockets would probably be a better option. Vaporizing the asteroid wouldn’t accomplish much, even if you could do it; what you actually want to do is impart as much sideways momentum as possible.

What I’m saying probably sounds extreme. It may even seem unjust or irrational. But look at those numbers again. Think carefully about the value of a human life. When we are talking about a risk of total human extinction, this is what rationality looks like. Zero tolerance for drug abuse or even terrorism is a ridiculous policy that does more harm than good. Zero tolerance for risk of nuclear war may be the only hope for humanity’s ongoing survival.

Throughout the vastness of the universe, there are probably billions of civilizations—I need only assume one civilization for every hundred galaxies. Of the civilizations that were unwilling to adopt zero tolerance policies on weapons of mass destruction and bear any cost, however unthinkable, to prevent their own extinction, there is almost boundless diversity, but they all have one thing in common: None of them will exist much longer. The only civilizations that last are the ones that refuse to tolerate weapons of mass destruction.

Daylight Savings Time is pointless and harmful

PNRJ current events, public policy , , , , , , ,

Nov 12, JDN 2458069

As I write this, Daylight Savings Time has just ended.

Sleep deprivation costs the developed world about 2% of GDP—on the order of $1 trillion per year. The US alone loses enough productivity from sleep deprivation that recovering this loss would give us enough additional income to end world hunger.

So, naturally, we have a ritual every year where we systematically impose an hour of sleep deprivation on the entire population for six months. This makes sense somehow.
The start of Daylight Savings Time each year is associated with a spike in workplace injuries, heart attacks, and suicide.

Nor does the “extra” hour of sleep we get in the fall compensate; in fact, it comes with its own downsides. Pedestrian fatalities spike immediately after the end of Daylight Savings Time; the rate of assault also rises at the end of DST, though it does also seem to fall when DST starts.

Daylight Savings Time was created to save energy. It does do that… technically. The total energy savings for the United States due to DST amounts to about 0.3% of our total electricity consumption. In some cases it can even increase energy use, though it does seem to smooth out electricity consumption over the day in a way that is useful for solar and wind power.

But this is a trivially small amount of energy savings, and there are far better ways to achieve it.

Simply due to new technologies and better policies, manufacturing in the US has reduced its energy costs per dollar of output by over 4% in the last few years. Simply getting all US states to use energy as efficiently as it is used in New York or California (not much climate similarity between those two states, but hmm… something about politics comes to mind…) would cut our energy consumption by about 30%.

The total amount of energy saved by DST is comparable to the amount of electricity now produced by small-scale residential photovoltaics—so simply doubling residential solar power production (which we’ve been doing every few years lately) would yield the same benefits as DST without the downsides. If we really got serious about solar power and adopted the policies necessary to get a per-capita solar power production comparable to Germany (not a very sunny place, mind you—Sacramento gets over twice the hours of sun per year that Berlin does), we would increase our solar power production by a factor of 10—five times the benefits of DST, none of the downsides.

Alternatively we could follow France’s model and get serious about nuclear fission. France produces over three hundred times as much energy from nuclear power as the US saves via Daylight Savings Time. Not coincidentally, France produces half as much CO2 per dollar of GDP as the United States.

Why would we persist in such a ridiculous policy, with such terrible downsides and almost no upside? To a first approximation, all human behavior is social norms.

Demystifying dummy variables

PNRJ statistics , , , ,

Nov 5, JDN 2458062

Continuing my series of blog posts on basic statistical concepts, today I’m going to talk about dummy variables. Dummy variables are quite simple, but for some reason a lot of people—even people with extensive statistical training—often have trouble understanding them. Perhaps people are simply overthinking matters, or making subtle errors that end up having large consequences.

A dummy variable (more formally a binary variable) is a variable that has only two states: “No”, usually represented 0, and “Yes”, usually represented 1. A dummy variable answers a single “Yes or no” question. They are most commonly used for categorical variables, answering questions like “Is the person’s race White?” and “Is the state California?”; but in fact almost any kind of data can be represented this way: We could represent income using a series of dummy variables like “Is your income greater than $50,000?” “Is your income greater than $51,000?” and so on. As long as the number of possible outcomes is finite—which, in practice, it always is—the data can be represented by some (possibly large) set of dummy variables. In fact, if your data set is large enough, representing numerical data with dummy variables can be a very good thing to do, as it allows you to account for nonlinear effects without assuming some specific functional form.
Most of the misunderstanding regarding dummy variables involves applying them in regressions and interpreting the results.
Probably the most common confusion is about what dummy variables to include. When you have a set of categories represented in your data (e.g. one for each US state), you want to include dummy variables for all but one of them. The most common mistake here is to try to include all of them, and end up with a regression that doesn’t make sense, or if you have a catchall category like “Other” (e.g. race is coded as “White/Black/Other”), leaving out that one and getting results with a nonsensical baseline.

You don’t have to leave one out if you only have one set of categories and you don’t include a constant in your regression; then the baseline will emerge automatically from the regression. But this is dangerous, as the interpretation of the coefficients is no longer quite so simple.

The thing to keep in mind is that a coefficient on a dummy variable is an effect of a change—so the coefficient on “White” is the effect of being White. In order to be an effect of a change, that change must be measured against some baseline. The dummy variable you exclude from the regression is the baseline—because the effect of changing to the baseline from the baseline is by definition zero.
Here’s a very simple example where all the regressions can be done by hand. Suppose you have a household with 1 human and 1 cat, and you want to know the effect of species on number of legs. (I mean, hopefully this is something you already know; but that makes it a good illustration.) In what follows, you can safely skip the matrix algebra; but I included it for any readers who want to see how these concepts play out mechanically in the math.
Your outcome variable Y is legs: The human has 2 and the cat has 4. We can write this as a matrix:

\[ Y = \begin{bmatrix} 2 \\ 4 \end{bmatrix} \]

reg_1

What dummy variables should we choose? There are actually several options.

 

The simplest option is to include both a human variable and a cat variable, and no constant. Let’s put the human variable first. Then our human subject has a value of X1 = [1 0] (“Yes” to human and “No” to cat) and our cat subject has a value of X2 = [0 1].

This is very nice in this case, as it makes our matrix of independent variables simply an identity matrix:

\[ X = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \]

reg_2

This makes the calculations extremely nice, because transposing, multiplying, and inverting an identity matrix all just give us back an identity matrix. The standard OLS regression coefficient is B = (X’X)-1 X’Y, which in this case just becomes Y itself.

\[ B = (X’X)^{-1} X’Y = Y = \begin{bmatrix} 2 \\ 4 \end{bmatrix} \]

reg_3

Our coefficients are 2 and 4. How would we interpret this? Pretty much what you’d think: The effect of being human is having 2 legs, while the effect of being a cat is having 4 legs. This amounts to choosing a baseline of nothing—the effect is compared to a hypothetical entity with no legs at all. And indeed this is what will happen more generally if you do a regression with a dummy for each category and no constant: The baseline will be a hypothetical entity with an outcome of zero on whatever your outcome variable is.
So far, so good.

But what if we had additional variables to include? Say we have both cats and humans with black hair and brown hair (and no other colors). If we now include the variables human, cat, black hair, brown hair, we won’t get the results we expect—in fact, we’ll get no result at all. The regression is mathematically impossible, regardless of how large a sample we have.

This is why it’s much safer to choose one of the categories as a baseline, and include that as a constant. We could pick either one; we just need to be clear about which one we chose.

Say we take human as the baseline. Then our variables are constant and cat. The variable constant is just 1 for every single individual. The variable cat is 0 for humans and 1 for cats.

Now our independent variable matrix looks like this:

\[ X = \begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \]

reg_4
The matrix algebra isn’t quite so nice this time:

\[ X’X = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} = \begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix} \]

\[ (X’X)^{-1} = \begin{bmatrix} 1 & -1 \\ -1 & 2 \end{bmatrix} \]

\[ X’Y = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 2 \\ 4 \end{bmatrix} = \begin{bmatrix} 6 \\ 4 \end{bmatrix} \]

\[ B = (X’X)^{-1} X’Y = \begin{bmatrix} 1 & -1 \\ -1 & 2 \end{bmatrix} \begin{bmatrix} 6 \\ 4 \end{bmatrix} = \begin{bmatrix} 2 \\ 2 \end{bmatrix} \]

reg_5

Our coefficients are now 2 and 2. Now, how do we interpret that result? We took human as the baseline, so what we are saying here is that the default is to have 2 legs, and then the effect of being a cat is to get 2 extra legs.
That sounds a bit anthropocentric—most animals are quadripeds, after all—so let’s try taking cat as the baseline instead. Now our variables are constant and human, and our independent variable matrix looks like this:

\[ X = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \]

\[ X’X = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix} \]

\[ (X’X)^{-1} = \begin{bmatrix} 1 & -1 \\ -1 & 2 \end{bmatrix} \]

\[ X’Y = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 2 \\ 4 \end{bmatrix} = \begin{bmatrix} 6 \\ 2 \end{bmatrix} \]

\[ B = \begin{bmatrix} 1 & -1 \\ -1 & 2 \end{bmatrix} \begin{bmatrix} 6 \\ 2 \end{bmatrix} = \begin{bmatrix} 4 \\ -2 \end{bmatrix} \]

reg_6

Our coefficients are 4 and -2. This seems much more phylogenetically correct: The default number of legs is 4, and the effect of being human is to lose 2 legs.
All these regressions are really saying the same thing: Humans have 2 legs, cats have 4. And in this particular case, it’s simple and obvious. But once things start getting more complicated, people tend to make mistakes even on these very simple questions.

A common mistake would be to try to include a constant and both dummy variables: constant human cat. What happens if we try that? The matrix algebra gets particularly nasty, first of all:

\[ X = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix} \]

\[ X’X = \begin{bmatrix} 1 & 1 \\ 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 2 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix} \]

reg_7

Our covariance matrix X’X is now 3×3, first of all. That means we have more coefficients than we have data points. But we could throw in another human and another cat to fix that problem.

 

More importantly, the covariance matrix is not invertible. Rows 2 and 3 add up together to equal row 1, so we have a singular matrix.

If you tried to run this regression, you’d get an error message about “perfect multicollinearity”. What this really means is you haven’t chosen a valid baseline. Your baseline isn’t human and it isn’t cat; and since you included a constant, it isn’t a baseline of nothing either. It’s… unspecified.

You actually can choose whatever baseline you want for this regression, by setting the constant term to whatever number you want. Set a constant of 0 and your baseline is nothing: you’ll get back the coefficients 0, 2 and 4. Set a constant of 2 and your baseline is human: you’ll get 2, 0 and 2. Set a constant of 4 and your baseline is cat: you’ll get 4, -2, 0. You can even choose something weird like 3 (you’ll get 3, -1, 1) or 7 (you’ll get 7, -5, -3) or -4 (you’ll get -4, 6, 8). You don’t even have to choose integers; you could pick -0.9 or 3.14159. As long as the constant plus the coefficient on human add to 2 and the constant plus the coefficient on cat add to 4, you’ll get a valid regression.
Again, this example seems pretty simple. But it’s an easy trap to fall into if you don’t think carefully about what variables you are including. If you are looking at effects on income and you have dummy variables on race, gender, schooling (e.g. no high school, high school diploma, some college, Bachelor’s, master’s, PhD), and what state a person lives in, it would be very tempting to just throw all those variables into a regression and see what comes out. But nothing is going to come out, because you haven’t specified a baseline. Your baseline isn’t even some hypothetical person with $0 income (which already doesn’t sound like a great choice); it’s just not a coherent baseline at all.

Generally the best thing to do (for the most precise estimates) is to choose the most common category in each set as the baseline. So for the US a good choice would be to set the baseline as White, female, high school diploma, California. Another common strategy when looking at discrimination specifically is to make the most privileged category the baseline, so we’d instead have White, male, PhD, and… Maryland, it turns out. Then we expect all our coefficients to be negative: Your income is generally lower if you are not White, not male, have less than a PhD, or live outside Maryland.

This is also important if you are interested in interactions: For example, the effect on your income of being Black in California is probably not the same as the effect of being Black in Mississippi. Then you’ll want to include terms like Black and Mississippi, which for dummy variables is the same thing as taking the Black variable and multiplying by the Mississippi variable.

But now you need to be especially clear about what your baseline is: If being White in California is your baseline, then the coefficient on Black is the effect of being Black in California, while the coefficient on Mississippi is the effect of being in Mississippi if you are White. The coefficient on Black and Mississippi is the effect of being Black in Mississippi, over and above the sum of the effects of being Black and the effect of being in Mississippi. If we saw a positive coefficient there, it wouldn’t mean that it’s good to be Black in Mississippi; it would simply mean that it’s not as bad as we might expect if we just summed the downsides of being Black with the downsides of being in Mississippi. And if we saw a negative coefficient there, it would mean that being Black in Mississippi is even worse than you would expect just from summing up the effects of being Black with the effects of being in Mississippi.

As long as you choose your baseline carefully and stick to it, interpreting regressions with dummy variables isn’t very hard. But so many people forget this step that they get very confused by the end, looking at a term like Black female Mississippi and seeing a positive coefficient, and thinking that must mean that life is good for Black women in Mississippi, when really all it means is the small mercy that being a Black woman in Mississippi isn’t quite as bad as you might think if you just added up the effect of being Black, plus the effect of being a woman, plus the effect of being Black and a woman, plus the effect of living in Mississippi, plus the effect of being Black in Mississippi, plus the effect of being a woman in Mississippi.