rent control

Home price targeting

PNRJ inequality, public policy , , , , , , , , , , ,

Jan 29 JDN 2459973

One of the largest divides in opinion between economists and the general population concerns the question of rent control. While the general public mostly supports rent control (and often votes for it in referenda), economists almost universally oppose it. It’s hard to get a consensus among economists on almost anything, and yet here we have one; but people don’t seem to care.

Why? I think it’s because high rents are a genuine and serious problem, which economists have invested remarkably little effort in trying to solve. Housing prices are one of the chief drivers of long-term inflation, and with most people spending over a third of their income on housing, even relatively small increases in housing prices can cause a lot of suffering.

One thing we do know is that rent control does not work as a long-term solution. Maybe in response to some short-term shock it would make sense. Maybe you do it for awhile as you wait for better long-term solutions to take effect. But simply putting an arbitrary cap on prices will create shortages in the long run—and it is not a coincidence that cities with strict rent control have the worst housing shortages and the greatest rates of homelessness. Rent control doesn’t even do a good job of helping the people who need it most.

Price ceilings in general are just… not a good idea. If people are selling something at a price that you think is too high and you just insist that they aren’t allowed to, they don’t generally sell at a lower price—they just don’t sell at all. There are a few exceptions; in a very monopolistic market, a well-targeted price ceiling might actually work. And short-run housing supply is inelastic enough that rent control isn’t the worst kind of price ceiling. But as a general strategy, price ceilings just aren’t an effective way of making things cheaper.

This is why we so rarely use them as a policy intervention. When the Federal Reserve wants to achieve a certain interest rate on bonds, do they simply demand that people buy the bonds at that price? No. They adjust the supply of bonds in the market until the market price goes to what they want it to be.

Prices aren’t set in a vacuum by the fiat of evil corporations. They are an equilibrium outcome of a market system. There are things you can do to intervene and shift that equilibrium, but if you just outlaw certain prices, it will result in a new equilibrium—it won’t simply be the same amount sold at the new price you wanted.

Maybe some graphs would help explain this. In each graph, the red line is the demand and the blue line is the supply.

Here is what the market looks like before intervention: The price is $6. We’ll say that’s too high; people can’t afford it.

[no_intervention.png]

Now suppose we impose a price ceiling at $4 (the green line). You aren’t allowed to charge more than $4. What will happen? Companies will charge $4. But they will also produce and sell a smaller quantity than before.

Far better would be to increase the supply of the good, shifting to a new supply curve (the purple line). Then you would reduce the price and increase the amount of the good available.

[supply_intervention.png]

This is precisely what we do with government bonds when we want to raise interest rates. (A greater supply of bonds makes their prices lower, which makes their yields higher.) And when we want to lower interest rates, we do the opposite.

Of course, with bonds, it’s easy to control the supply; it’s all just numbers in a network. Increasing the supply of housing is a much greater undertaking; you actually need to build new housing. But ultimately, the only way to ensure that housing is available and affordable for everyone is in fact to build more housing.

There are various ways we might accomplish that; one of the simplest would be to simply relax zoning restrictions that make it difficult to build high-density housing in cities. Those are bad laws anyway; they only benefit a small number of people a little bit while harming a large number of people a lot. (The problem is that the people they benefit are the local homeowners who show up to city council meetings.)

But we could do much more. I propose that we really use interest-rate targeting as our model and introduce home price targeting. I want the federal government to exercise eminent domain and order the construction of new high-density housing in any city that has rents above a certain threshold—if you like, the same threshold you were thinking of setting the rent control at.

Is this an extreme solution? Perhaps. But housing affordability is an extreme problem. And I keep hearing from the left wing that economists aren’t willing to consider “radical enough” solutions to housing (by which they always seem to mean the tried-and-failed strategy of rent control). So here’s a radical solution for you. If cities refuse to build enough housing for their people, make them do it. Buy up and bulldoze their “lovely” “historic” suburban neighborhoods that are ludicrous wastes of land (and also environmentally damaging), and replace them with high-rise apartments. (Get rid of the golf courses while you’re at it.)

This would be expensive, of course; we have to pay to build all those new apartments. But hardly so expensive as living in a society where people can’t afford to live where they want.

In fact, estimates suggest that we are losing over one trillion dollars per year in unrealized productivity because people can’t afford to live in the highest-rent cities. Average income per worker in the US has been reduced by nearly $7000 per year because of high housing prices. So that’s the budget you should be comparing against. Keeping things as they are is like taxing our whole population about 9%. (And it’s probably regressive, so more than that for poor people.)

Would this destroy the “charm” of the city? I dunno, maybe a little. But if the only thing your city had going for it was some old houses that are clearly not an efficient use of space, that’s pretty sad. And it is quite possible to build a city at high density and have it still be beautiful and a major draw for tourists; Paris is a lot denser than far-less-picturesque Houston. (Though I’ll admit, Houston is far more affordable than Paris. It’s not just about density.) And is the “charm” of your city really worth making it so unaffordable that people can’t move there without risking becoming homeless?

There are a lot of details to be worked out: How serious must things get before the federal government steps in? (Wherever we draw the line, San Francisco is surely well past it.) It takes a long time to build houses and let prices adjust, so how do we account for that time-lag? Where does the money come from, actually? Debt? Taxes? But these could all be resolved.

Of course, it’s a pipe dream; we’re never going to implement this policy, because homeowners dread the idea of their home values going down (even though it would actually make their property taxes cheaper!). I’d even be willing to consider some kind of program that would let people refinance underwater mortgages to write off the lost equity, if that’s what it takes to actually build enough housing.

Because there is really only one thing that’s ever going to solve the (global!) housing crises:

Build more homes.

Why will no one listen to economists on rent control?

PNRJ current events, inequality, market failure, public policy , , , , , , , ,

Sep 22 JDN 2458750

I am on the verge of planting my face into my desk, because California just implemented a statewide program of rent control. I understand the good intentions here; it is absolutely the case that housing in California is too expensive. There are castles in Spain cheaper than condos in California. But this is not the right solution. Indeed, it will almost certainly make the problem worse. Maybe housing prices won’t be too high; instead there simply won’t be enough homes and more people will live on the street. (It’s not a coincidence that the Bay Area has both some of the world’s tightest housing regulations and one of the highest rates of homelessness.)

There is some evidence that rent control can help keep tenants in their homes—but at the cost of reducing the overall housing supply. Most of the benefits of rent control actually fall upon the upper-middle-class, not the poor.

Price controls are in general a terrible way of intervening in the economy. Price controls are basically what destroyed Venezuela. In this case the ECON 101 argument is right: Put a cap on the price of something, and you will create a shortage of that thing. Always.

California makes this worse by including all sorts of additional regulations on housing construction. Some regulations are necessary—homes need to be safe to live in—but did we really need a “right to sunlight”? How important is “the feel of the city” compared to homelessness? Not every building needs its own parking! (That, at least, the state government seems to be beginning to understand.) And yes, we should be investing heavily in solar power, and rooftops are a decent place to put those solar panels; but you should be subsidizing solar panels, not mandating them and thereby adding the cost of solar panels to the price of every new building.

Of course, we can’t simply do nothing; we need to fix this housing crisis. But there are much better ways of doing so. Again the answer is to subsidize rather than regulate.

Here are some policy options for making housing more affordable:

  1. Give every person below a certain income threshold a one-time cash payment to help them pay for a down payment or first month’s rent. Gradually phase out the payment as their income increases in the same way as the Earned Income Tax Credit.
  2. Provide a subsidy for new housing construction, with larger subsidies for buildings with smaller, more affordable apartments.
  3. Directly pay for the construction of new public housing.
  4. Relax zoning regulations to make construction less expensive.
  5. Redistribute income from the rich to the poor using progressive taxes and transfer payments. Housing crises are always and everywhere a problem of inequality.

Some of these would cost money, yes; we would probably need to raise taxes to pay for them. But rent control has costs too. We are already paying these costs, but instead of paying them in the form of taxes that can be concentrated on the rich, we pay them in the form of a housing crisis that hurts the poor most of all.

The weirdest thing about all this is that any economist would agree.

Economists can be a contentious bunch: It has been said that if you ask five economists a question, you’ll get five answers—six if one is from Harvard. Yet the consensus among economists against rent control is absolutely overwhelming. Analyses of journal articles and polls of eminent economists suggest that over 90% of economists, regardless of their other views or their political leanings, agree that rent control is a bad idea.

This is a staggering result: There are economists who think that almost all taxes and regulations are fundamentally evil and should all be removed, and economists who think that we need radical, immediate government intervention to prevent a global climate catastrophe. But they all agree that rent control is a bad idea.

Economists differ in their views about legacy college admissions, corporate antitrust, wealth taxes, corporate social responsibility, equal pay for women, income taxes, ranked-choice voting, the distributional effects of monetary policy, the relation between health and economic growth, minimum wage, and healthcare spending. They disagree about whether Christmas is a good thing! But they all agree that rent control is a bad idea.

We’re not likely to ever get a consensus much better than this in any social science. The economic case against rent control is absolutely overwhelming. Why aren’t policymakers listening to us?

I really would like to know. It’s not that economists have ignored the problem of housing affordability. We have suggested a variety of other solutions that would obviously be better than rent control—in fact, I just did, earlier in this post. Many of them would require tax money, yes—do you want to fix this problem, or not?

Maybe that’s it: Maybe policymakers don’t really care about making housing affordable. If they did, they’d be willing to bear the cost of raising taxes on millionaires in order to build more apartments and keep people from being homeless. But they want to seem like they care about making housing affordable, because they know their constituents care. So they use a policy that seems to make housing more affordable, even though it doesn’t actually work, because that policy also doesn’t affect the government budget (at least not obviously or directly—of course it still does indirectly). They want the political support of the poor, who think this will help them; and they also want the political support of the rich, who refuse to pay a cent more in taxes.

But it really makes me wonder what we as economists are even really doing: If the evidence is this clear and the consensus is this overwhelming, and policymakers still ignore us—then why even bother?

Downsides of rent control

PNRJ market failure, public policy, Uncategorized , , , , ,

May 13 JDN 2458252

One of the largest ideological divides between economists and the rest of the population concerns rent control.

Tent control is very popular among the general population, especially in California—with support hovering around 60% in Orange County, San Diego County, and across California in general. About 60% of people in the UK and over 50% in Ontario, Canada also support rent control.

Meanwhile, economists overwhelmingly oppose rent control: When evaluating the statement “A ceiling on rents reduces the quantity and quality of housing available.”, over 76% of economists agreed, and 16% agreed with qualifications. For the record, I would be an “agree with qualifications” as well (as they say, there are few one-handed economists).

There is evidence of some benefits of rent control, at least for the small number of people who can actually manage to stay in rent-controlled units. People who live in rent-controlled units are about 15% more likely to stay where they are, even in places as expensive as San Francisco, which could be considered a good thing (though I’m not convinced it always is; mobility is one of the key forces driving the dynamism of the US economy).

But there are winners and losers. Landlords whose properties are rent-controlled decreased their supply of housing by an average of 15%, via a combination of converting them to condos, removing them from the market, or demolishing the buildings outright. As a result, rent control increases average rent in a city by an average of 5%. One of the most effective ways to get out of rent control is to remove a building from the market entirely; this allows you to evict all of your tenants with very little notice, and is responsible for thousands of tenants being evicted every year in Los Angeles.

Rent control disincentivizes both new housing construction and the proper maintenance of existing housing. The quality of rent-controlled homes is systematically lower than the quality of other homes.

The benefits of rent control mainly fall upon the upper-middle class, not the poor. Rent control can make an area more racially diverse—but it benefits middle-class members of racial minorities, not poor members. Most of the benefits of rent control go to older families who have lived in a city for a long time—which makes them a transfer of wealth away from young people.

Cities such as Chicago without rent control systematically have lower rents, not higher; partly this is a cause, rather than an effect, as tenants are less likely to panic and demand rent control when rents are not high. But it’s also an effect, as rent control holds down the price in part of the market but ends up driving it up in the rest. Over 40% of San Francisco’s apartments are rent-controlled, and they have the highest rents in the world.

Rent control also contributes to the tendency toward building high-end luxury apartments; if you know that you will never be able to raise the rent on your existing buildings, and may end up being stuck with whatever rent you charge the first year on your new buildings, you have a strong reason to want to charge as much as possible the first year you build new apartments. Rent control also creates subtler distortions in the size and location of apartment construction. The effects of rent control even spill over into other housing markets, such as owner-occupied homes and mobile homes.
Because it locks people into place and reduces the construction of new homes near city centers, rent control increases commute times and carbon emissions. This is probably something we should especially point out to people in California, as the two things Californians hate most are environmental degradation and traffic congestion. (Then again, the third is high rent.) California is good at avoiding the first one—our GDP/carbon emission ratio is near the best in the US. The other two? Not so much.

Of course, simply removing rent control would not immediately solve the housing shortage; while it would probably have benefits in the long run, during the transition period a lot of people currently protected by rent control would lose their homes. Even in the long run, it would probably not be enough to actually make rent affordable in the largest coastal cities.

But it’s vital not to confuse “lower rent” with “rent control”; there are much, much better ways to reduce rent prices than simply enforcing arbitrary caps on them.

We have learned not to use price controls in other markets, but not housing for some reason. Think about the gasoline market, for example. High gas prices are very politically unpopular (though frankly I never quite understood why; it’s a tiny fraction of consumption expenditure, and if we ever want to make a dent in our carbon emissions we need to make our gas prices much higher), but imagine how ridiculous it would seem for a politician to propose simply making an arbitrary cap that says you aren’t allowed to sell gasoline for more than $2.50 per gallon in a particular city. The obvious outcome would be for most gas stations in that city to immediately close, and everyone to end up buying their gas at the new gas stations that spring up just outside the city limits charging $4.00 per gallon. This is basically what happens in the housing market: Rent-controlled apartments apartments are taken off the market, and the new housing that is built ends up even more expensive.

In a future post, I’ll discuss things we can do instead of rent control that would reliably make housing more affordable. Most of these would involve additional government spending; but there are two things I’d like to say about that. First, we are already spending this money, we just don’t see it, because it comes in the form of inefficiencies and market distortions instead of a direct expenditure. Second, do we really care about making housing affordable, or not? If we really care, we should be willing to spend money on it. If we aren’t willing to spend money on it, then we must not really care.

What exactly is “gentrification”? How should we deal with it?

PNRJ development economics, ethics, inequality, market failure, public policy , , , , , , , , , , , , ,

Nov 26, JDN 2458083

“Gentrification” is a word that is used in a variety of mutually-inconsistent ways. If you compare the way social scientists use it to the way journalists use it, for example, they are almost completely orthogonal.

The word “gentrification” is meant to invoke the concept of a feudal gentry—a hereditary landed class that extracts rents from the rest of the population while contributing little or nothing themselves.

If indeed that is what we are talking about, then obviously this is bad. Moreover, it’s not an entirely unfounded fear; there are some remarkably strong vestiges of feudalism in the developed world, even in the United States where we never formally had a tradition of feudal titles. There really is a significant portion of the world’s wealth held by a handful of billionaire landowner families.

But usually when people say “gentrification” they mean something much broader. Almost any kind of increase in urban real estate prices gets characterized as “gentrification” by at least somebody, and herein lies the problem.

In fact, the kind of change that is most likely to get characterized as “gentrification” isn’t even the rising real estate prices we should be most worried about. People aren’t concerned when the prices of suburban homes double in 20 years. You might think that things that are already too expensive getting more expensive would be the main concern, but on the contrary, people are most likely to cry “gentrification” when housing prices rise in poor areas where housing is cheap.

One of the most common fears about gentrification is that it will displace local residents. In fact, the best quasi-experimental studies show little or no displacement effect. It’s actually mainly middle-class urbanites who get displaced by rising rents. Poor people typically own their homes, and actually benefit from rising housing prices. Young upwardly-mobile middle-class people move to cities to rent apartments near where they work, and tend to assume that’s how everyone lives, but it’s not. Rising rents in a city are far more likely to push out its grad students than they are poor families that have lived there for generations. Part of why displacement does not occur may be because of policies specifically implemented to fight it, such as subsidized housing and rent control. If that’s so, let’s keep on subsidizing housing (though rent control will always be a bad idea).

Nor is gentrification actually a very widespread phenomenon. The majority of poor neighborhoods remain poor indefinitely. In most studies, only about 30% of neighborhoods classified as “gentrifiable” actually end up “gentrifying”. Less than 10% of the neighborhoods that had high poverty rates in 1970 had low poverty rates in 2010.

Most people think gentrification reduces crime, but in the short run the opposite is the case. Robbery and larceny are higher in gentrifying neighborhoods. Criminals are already there, and suddenly they get much more valuable targets to steal from, so they do.

There is also a general perception that gentrification involves White people pushing Black people out, but this is also an overly simplistic view. First of all, a lot of gentrification is led by upwardly-mobile Black and Latino people. Black people who live in gentrified neighborhoods seem to be better off than Black people who live in non-gentrified neighborhoods; though selection bias may contribute to this effect, it can’t be all that strong, or we’d observe a much stronger displacement effect. Moreover, some studies have found that gentrification actually tends to increase the racial diversity of neighborhoods, and may actually help fight urban self-segregation, though it does also tend to increase racial polarization by forcing racial mixing.

What should we conclude from all this? I think the right conclusion is we are asking the wrong question.

Rising housing prices in poor areas aren’t inherently good or inherently bad, and policies designed specifically to increase or decrease housing prices are likely to have harmful side effects. What we need to be focusing on is not houses or neighborhoods but people. Poverty is definitely a problem, for sure. Therefore we should be fighting poverty, not “gentrification”. Directly transfer wealth from the rich to the poor, and then let the housing market fall where it may.

There is still some role for government in urban planning more generally, regarding things like disaster preparedness, infrastructure development, and transit systems. It may even be worthwhile to design regulations or incentives that directly combat racial segregation at the neighborhood level, for, as the Schelling Segregation Model shows, it doesn’t take a large amount of discriminatory preference to have a large impact on socioeconomic outcomes. But don’t waste effort fighting “gentrification”; directly design policies that will incentivize desegregation.

Rising rent as a proportion of housing prices is still bad, and the fundamental distortions in our mortgage system that prevent people from buying houses are a huge problem. But rising housing prices are most likely to be harmful in rich neighborhoods, where housing is already overpriced; in poor neighborhoods where housing is cheap, rising prices might well be a good thing.
In fact, I have a proposal to rapidly raise homeownership across the United States, which is almost guaranteed to work, directly corrects an enormous distortion in financial markets, and would cost about as much as the mortgage interest deduction (which should probably be eliminated, as most economists agree). Give each US adult a one-time grant voucher which gives them $40,000 that can only be spent as a down payment on purchasing a home. Each time someone turns 18, they get a voucher. You only get one over your lifetime, so use it wisely (otherwise the policy could become extremely expensive); but this is an immediate direct transfer of wealth that also reduces your credit constraint. I know I for one would be house-hunting right now if I were offered such a voucher. The mortgage interest deduction means nothing to me, because I can’t afford a down payment. Where the mortgage interest deduction is regressive, benefiting the rich more than the poor, this policy gives everyone the same amount, like a basic income.

In the short run, this policy would probably be expensive, as we’d have to pay out a large number of vouchers at once; but with our current long-run demographic trends, the amortized cost is basically the same as the mortgage interest deduction. And the US government especially should care about the long-run amortized cost, as it is an institution that has lasted over 200 years without ever missing a payment and can currently borrow at negative real interest rates.

Why is housing so expensive?

PNRJ market failure, public policy , , , , , , , , , , ,

Apr 30, JDN 2457874

It’s not your imagination: Housing is a lot more expensive than it used to be. Inflation adjusted into 2000 dollars, the median price of a house has risen from $30,600 in 1940 to $119,600 today. Adjusted to today’s dollars, that’s an increase from $44,000 to $173,000.

Things are particularly bad here in California, where the median price of a new home is $517,000—and especially in the Bay Area, where the median price is $838,000. Just two years ago, people were already freaking out that the median home price in the Bay Area had hit $661,000—and now it has risen 27% since then.

The rent is too damn high, but lately rent has actually not been rising as fast as housing prices. It may be that they’ve just gotten as high as they can get; in New York City rent is stable, and in San Francisco it’s actually declining—but in both cases it’s over $4,000 per month for a 2-bedroom apartment. The US still has the highest rent-to-price ratio in the world; at 11.2%, you should be able to buy a house on a 15-year mortgage for what we currently pay in rent near city centers.

But this is not a uniquely American problem.

It’s a problem in Canada: Housing in the Toronto area recently skyrocketed in price, with the mean price of a detached home now over $974,000 CAD, about $722,000 USD.

It’s a problem in the UK: The average price of a home in the UK is now over 214,000 pounds, or $274,000 (the pound is pretty weak after Brexit). In London in particular, the average home now costs nine years of the average wage.

It’s even a problem in China: An average 1000-square-foot apartment (that’s not very big!) in Shanghai now sells for 5 million yuan, which is about $725,000.

Worldwide, the US actually has a relatively low housing price to income ratio, because our incomes are so high. Venezuela’s economy is in such a terrible state that it is literally impossible for the average person to buy the average home, but in countries as diverse as France, Taiwan, and Peru, the average home still costs more than 10 years of the average household income.

Why is this happening? Why is housing so expensive, and getting worse all the time?

There are a lot of reasons that have been proposed.

The most obvious and fundamental reason is basic supply and demand. Demand for housing in major cities is rapidly rising, and supply of housing just isn’t keeping up.

Indeed, in California, the rate of new housing construction has fallen in recent years, even as we’ve had rapid population growth and skyrocketing housing prices. This is probably the number one reason why our housing here is so expensive.

But that raises its own questions: why aren’t more houses getting built? The market is supposed to correct for this sort of thing. Higher prices incentivize more construction, so prices get brought back down.

I think with housing in particular, we have a fundamental problem with that mechanism, and it is this: The people who make the policy don’t want the prices to come down.

No, I’m not talking about mayors and city councils, though they do like their property tax revenue. I’m talking about homeowners. People who go to homeowners’ association meetings and complain that someone else’s lopsided deck or un-weeded garden is “lowering property values”. People who join NIMBY political campaigns to stop new development, prevent the construction of taller buildings, or even stop the installation of new electrical substations. People who already got theirs and don’t care about anyone else.

Homeowners have an enormous influence in local politics, and it is by local politics that most of these decisions about zoning and development are made. They make all kinds of excuses about “preserving the community” and “the feel of the city”, but when you get right down to it, these people care more about preserving their own home equity than they do about making other people homeless.

In some cases, people may be so fundamentally confused that they think new development actually somehow causes higher housing prices, and so they try to fight development in a vain effort to stop rising housing prices and only end up making things worse. It’s also very common for people to support rent control policies in an effort to keep housing affordable—and economists of all political stripes are in almost total consensus that rent control only serves to restrict supply, increase inequality, and make housing prices even worse. As one might expect, the stricter the rent control, the worse this effect is. Some mild forms of rent control might be justifiable in particularly monopolistic markets, but in general it’s not a good long-term solution. Rent control forces rationing, and often the rationing is not in favor of who needs it the most but who is the most well-connected. The people who benefit most from rent control are usually of higher income than the average for the city.

On the other hand, removing rent control can cause a spike in prices, and make things worse in the short run, before there is time for new construction to increase the supply of housing. Also, many economists assume in their models that tenants who get forced out by the higher rents would get compensated for it, which is not at all how the real world works. It’s also unclear exactly how large the effect sizes are, because the empirical studies get quite mixed results. Still, rent control is a bad idea. Don’t take it from me, take it from Paul Krugman.

It’s also common to blame foreign investors—because humans are tribal, and blaming foreigners is always popular—even though that makes no economic sense. Investors are buying your houses because the prices keep rising. It’s possible that there could be some sort of speculative bubble, but that’s actually harder to sustain in housing than it is in most other assets, precisely because houses are immobile and expensive. Speculative bubbles in gold happen all the time (indeed, perhaps literally all the time, as the price of gold has never fallen to its real fundamental value in all of human history), but gold is a tradeable, transportable, fungible commodity that can be bought in arbitrarily small quantities. (Because it’s an element, you’re literally only limited to the atomic level!)

Moreover, it isn’t just supply and demand at work here. Fluctuations in economic growth have strong effects on housing prices—and vice-versa. There are monetary policy effects, particularly in a liquidity trap; lower interest rates combined with low inflation create a perfect storm for higher housing prices.

Overall economic inequality is a major contributor to steep housing prices, as well as the segregation of housing across racial and economic lines. And as the rate of return on productive capital continues to decrease while the rate of return on real estate does not, more and more of our wealth concentration is going to be in the form of higher housing prices—making the whole problem self-reinforcing.

People also seem really ambivalent about whether they want housing prices to be low or high. In one breath they’ll bemoan the lack of affordable housing, and in another they’ll talk about “protecting property values”. Even the IMF called the increase in housing prices after the Second Depression a “recovery”. Is it really so hard to understand that higher prices mean higher prices?

But we think of housing as two fundamentally different things. On the one hand, it’s a durable consumption good, like a car or a refrigerator—something you buy because it’s useful, and keep around to use for a long time. On the other hand, it’s a financial asset—a store of value for your savings and a potential source of income. When you’re thinking of it as a consumption good, you want it to be “affordable”; when you’re thinking of it as an asset, you want to “protect its value”. But it’s the same house with the same price. You can’t do both of those things at once, and clearly, as a society—perhaps as a civilization—we have been tilting way too far in the “asset” direction.

I get it: Financial assets that grow over time have the allure of easy money. The stock market, the derivatives market, even the lottery and Las Vegas, all have this tantalizing property that they seem to give you money for nothing. They are like the quest for the Philosopher’s Stone in days of yore.

But they are just as much a chimera as the Philosopher’s Stone itself. (Also, if anyone had found the Philosopher’s Stone, the glut of gold would have triggered massive inflation, not unlike what happened in Spain in the 16th century.) Any money you get from simply owning an asset or placing a bet is money that had to come from somewhere else. In the case of the stock market, that “somewhere else” is the profits of the corporations you bought, and if you did actually contribute to the investment of those corporations there’s nothing wrong with you getting a proportional share of those profits. But most people aren’t thinking in those terms when they buy stocks, and once you get all the way to sophisticated derivatives you’re basically in full gambling territory. Every option that’s in the money is another option that’s out of the money. Every interest rate swap that turns a profit is another one that bears a loss.

And when it comes to housing, if you magically gain equity from rising property values, where is that money coming from? It’s coming from people desperately struggling to afford to live in your city, people giving up 40%, 50%, even 60% of their disposable income just for the chance to leave in a tiny apartment because they want to be in your city that badly. It’s coming from people who started that way, lost their job, and ended up homeless because they couldn’t sustain the payments anymore. All that easy money is coming from hard-working young people trying to hold themselves out of poverty.

It’s different if your home gains value because you actually did something to make it better—renovations, additions, landscaping. Even then I think these things are sort of overrated; but they do constitute a real economic benefit to the people who live there. But if your home rises in value because zoning regulations and protesting homeowners stop the construction of new high-rises, that’s very much still on the backs of struggling young people.

We need to stop thinking houses as assets that are supposed to earn a return, and instead think of them as consumption goods that provide benefits to people. If you want a return, buy stocks and bonds. When you’re buying a house, you should be buying a house—not some dream of making money for nothing as housing prices rise forever. Because they can’t—sooner or later, the bubble will break—and even if they could, it would be terrible for everyone who didn’t get into the market soon enough.

Elasticity and the Law of Supply

PNRJ core principles, public policy , , , , , , , , , , , , , , , ,

JDN 2457292 EDT 16:16.

Today’s post is kind of a mirror image of the previous post earlier this week; I was talking about demand before, and now I’m talking about supply. (In the next post, I’ll talk about how the two work together to determine the actual price of goods.)

Just as there is an elasticity of demand which describes how rapidly the quantity demanded changes with changes in price, likewise there is an elasticity of supply which describes how much the quantity supplied changes with changes in price.

The elasticity of supply is defined as the proportional change in quantity supplied divided by the proportional change in price; so for example if the number of cars produced increases 10% when the price of cars increases by 5%, the elasticity of supply of cars would be 10%/5% = 2.

Goods that have high elasticity of supply will rapidly flood the market if the price increases even a small amount; goods that have low elasticity of supply will sell at about the same rate as ever even if the price increases dramatically.

Generally, the more initial investment of capital a good requires, the lower its elasticity of supply is going to be.

If most of the cost of production is in the actual marginal cost of producing each new gizmo, then elasticity of supply will be high, because it’s easy to produce more or produce less as the market changes.

But if most of the cost is in building machines or inventing technologies or training employees which already has to be done in order to make any at all, while the cost of each individual gizmo is unimportant, the elasticity of supply will be low, because there’s no sense letting all that capital you invested go to waste.
We can see these differences in action by comparing different sources of electric power.

Photovoltaic solar power has a high elasticity of supply, because building new solar panels is cheap and fast. As the price of solar energy fluctuates, the amount of solar panel produced changes rapidly. Technically this is actually a “fixed capital” cost, but it’s so modular that you can install as little or as much solar power capacity as you like, which makes it behave a lot more like a variable cost than a fixed cost. As a result, a 1% increase in the price paid for solar power increases the amount supplied by a whopping 2.7%, a supply elasticity of 2.7.

Oil has a moderate elasticity of supply, because finding new oil reserves is expensive but feasible. A lot of oil in the US is produced by small wells; 18% of US oil is produced by wells that put out less than 10 barrels per day. Those small wells can be turned on and off as the price of oil changes, and new ones can be built if it becomes profitable. As a result, investment in oil production is very strongly correlated with oil prices. Still, overall production of oil changes only moderate amounts; in the US it had been steadily decreasing since 1970 until very recently when new technologies and weakened regulations resulted in a rapid increase to near-1970s levels. We sort of did hit peak oil; but it’s never quite that simple.

Nuclear fission has a very low elasticity of supply, because building a nuclear reactor is extremely expensive and requires highly advanced expertise. Building a nuclear power plant costs upward of $35 billion. Once a reactor is built, the cost of generating more power is relatively trivial; three-fourths of the cost a nuclear power plant will ever pay is paid simply to build it (or to pay back the debt incurred by doing so). Even if the price of uranium plummets or the price of oil skyrockets, it would take a long time before more nuclear power plants would be built in response.

Elasticity of supply is generally a lot larger in the long run than in the short run. Over a period of a few days or months, many types of production can’t be changed significantly. If you have a corn field, you grow as much corn as you can this season; even if the price rose substantially you couldn’t actually grow any more than your field will allow. But over a period of a year to a few years, most types of production can be changed; continuing with the corn example, you could buy new land to plant corn next season.

The Law of Supply is actually a lot closer to a true law than the Law of Demand. A negative elasticity of supply is almost unheard of; at worst elasticity of supply can sometimes drop close to zero. It really is true that elasticity of supply is almost always positive.

Land has an elasticity near zero; it’s extremely expensive (albeit not impossible; Singapore does it rather frequently) to actually create new land. As a result there’s really no good reason to ever raise the price of land; higher land prices don’t incentivize new production, they just transfer wealth to landowners. That’s why a land tax is such a good idea; it would transfer some of that wealth away from landowners and let us use it for public goods like infrastructure or research, or even just give it to the poor. A few countries actually have tried this; oddly enough, they include Singapore and Denmark, two of the few places in the world where the elasticity of land supply is appreciably above zero!

Real estate in general (which is what most property taxes are imposed on) is much trickier: In the short run it seems to have a very low elasticity, because building new houses or buildings takes a lot of time and money. But in the long run it actually has a high elasticity of supply, because there is a lot of profit to be made in building new structures if you can fund projects 10 or 15 years out. The short-run elasticity is something like 0.2, meaning a 1% increase in price only yields a 0.2% increase in supply; but the long-run elasticity may be as high as 8, meaning that a 1% increase in price yields an 8% increase in supply. This is why property taxes and rent controls seem like a really good idea at the time but actually probably have the effect of making housing more expensive. The economics of real estate has a number of fundamental differences from the economics of most other goods.

Many important policy questions ultimately hinge upon the elasticity of supply: If elasticity is high, then taxing or regulating something is likely to cause large distortions of the economy, while if elasticity is low, taxes and regulations can be used to support public goods or redistribute wealth without significant distortion to the economy. On the other hand, if elasticity is high, markets generally function well on their own, while if elasticity is low, prices can get far out of whack. As a general rule of thumb, government intervention in markets is most useful and most necessary when elasticity is low.

What you need to know about tax incidence

PNRJ core principles, public policy, Top 10 things to know about economics , , , , , , , , , , , , , ,

JDN 2457152 EDT 14:54.

I said in my previous post that I consider tax incidence to be one of the top ten things you should know about economics. If I actually try to make a top ten list, I think it goes something like this:

  1. Supply and demand
  2. Monopoly and oligopoly
  3. Externalities
  4. Tax incidence
  5. Utility, especially marginal utility of wealth
  6. Pareto-efficiency
  7. Risk and loss aversion
  8. Biases and heuristics, including sunk-cost fallacy, scope neglect, herd behavior, anchoring and representative heuristic
  9. Asymmetric information
  10. Winner-takes-all effect

So really tax incidence is in my top five things you should know about economics, and yet I still haven’t talked about it very much. Well, today I will. The basic principles of supply and demand I’m basically assuming you know, but I really should spend some more time on monopoly and externalities at some point.

Why is tax incidence so important? Because of one central fact: The person who pays the tax is not the person who writes the check.

It doesn’t matter whether a tax is paid by the buyer or the seller; it matters what the buyer and seller can do to avoid the tax. If you can change your behavior in order to avoid paying the tax—buy less stuff, or buy somewhere else, or deduct something—you will not bear the tax as much as someone else who can’t do anything to avoid the tax, even if you are the one who writes the check. If you can avoid it and they can’t, other parties in the transaction will adjust their prices in order to eat the tax on your behalf.

Thus, if you have a good that you absolutely must buy no matter what—like, say, table salt—and then we make everyone who sells that good pay an extra $5 per kilogram, I can guarantee you that you will pay an extra $5 per kilogram, and the suppliers will make just as much money as they did before. (A salt tax would be an excellent way to redistribute wealth from ordinary people to corporations, if you’re into that sort of thing. Not that we have any trouble doing that in America.)

On the other hand, if you have a good that you’ll only buy at a very specific price—like, say, fast food—then we can make you write the check for a tax of an extra $5 per kilogram you use, and in real terms you’ll pay hardly any tax at all, because the sellers will either eat the cost themselves by lowering the prices or stop selling the product entirely. (A fast food tax might actually be a good idea as a public health measure, because it would reduce production and consumption of fast food—remember, heart disease is one of the leading causes of death in the United States, making cheeseburgers a good deal more dangerous than terrorists—but it’s a bad idea as a revenue measure, because rather than pay it, people are just going to buy and sell less.)

In the limit in which supply and demand are both completely fixed (perfectly inelastic), you can tax however you want and it’s just free redistribution of wealth however you like. In the limit in which supply and demand are both locked into a single price (perfectly elastic), you literally cannot tax that good—you’ll just eliminate production entirely. There aren’t a lot of perfectly elastic goods in the real world, but the closest I can think of is cash. If you instituted a 2% tax on all cash withdrawn, most people would stop using cash basically overnight. If you want a simple way to make all transactions digital, find a way to enforce a cash tax. When you have a perfect substitute available, taxation eliminates production entirely.

To really make sense out of tax incidence, I’m going to need a lot of a neoclassical economists’ favorite thing: Supply and demand curves. These things pop up everywhere in economics; and they’re quite useful. I’m not so sure about their application to things like aggregate demand and the business cycle, for example, but today I’m going to use them for the sort of microeconomic small-market stuff that they were originally designed for; and what I say here is going to be basically completely orthodox, right out of what you’d find in an ECON 301 textbook.

Let’s assume that things are linear, just to make the math easier. You’d get basically the same answers with nonlinear demand and supply functions, but it would be a lot more work. Likewise, I’m going to assume a unit tax on goods—like $2890 per hectare—as opposed to a proportional tax on sales—like 6% property tax—again, for mathematical simplicity.

The next concept I’m going to have to talk about is elasticity—which is the proportional amount that quantity sold changes relative to price. If price increases 2% and you buy 4% less, you have a demand elasticity of -2. If price increases 2% and you buy 1% less, you have a demand elasticity of -1/2. If price increases 3% and you sell 6% more, you have a supply elasticity of 2. If price decreases 5% and you sell 1% less, you have a supply elasticity of 1/5.

Elasticity doesn’t have any units of measurement, it’s just a number—which is part of why we like to use it. It also has some very nice mathematical properties involving logarithms, but we won’t be needing those today.

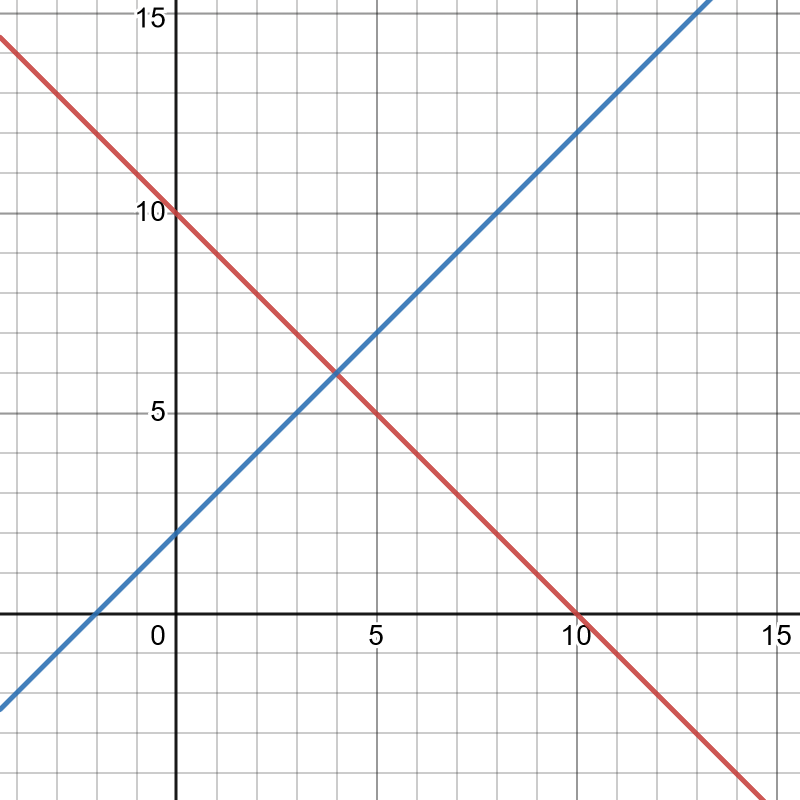
The price that renters are willing and able to pay, the demand price PD will start at their maximum price, the reserve price PR, and then it will decrease linearly according to the quantity of land rented Q, according to a linear function (simply because we assumed that) which will vary according to a parameter e that represents the elasticity of demand (it isn’t strictly equal to it, but it’s sort of a linearization).

We’re interested in what is called the consumer surplus; it is equal to the total amount of value that buyers get from their purchases, converted into dollars, minus the amount they had to pay for those purchases. This we add to the producer surplus, which is the amount paid for those purchases minus the cost of producing them—which is basically just the same thing as profit. Togerther the consumer surplus and producer surplus make the total economic surplus, which economists generally try to maximize. Because different people have different marginal utility of wealth, this is actually a really terrible idea for deep and fundamental reasons—taking a house from Mitt Romney and giving it to a homeless person would most definitely reduce economic surplus, even though it would obviously make the world a better place. Indeed, I think that many of the problems in the world, particularly those related to inequality, can be traced to the fact that markets maximize economic surplus rather than actual utility. But for now I’m going to ignore all that, and pretend that maximizing economic surplus is what we want to do.

You can read off the economic surplus straight from the supply and demand curves; it’s the area between the lines. (Mathematically, it’s an integral; but that’s equivalent to the area under a curve, and with straight lines they’re just triangles.) I’m going to call the consumer surplus just “surplus”, and producer surplus I’ll call “profit”.

Below the demand curve and above the price is the surplus, and below the price and above the supply curve is the profit:

elastic_supply_competitive_labeled

I’m going to be bold here and actually use equations! Hopefully this won’t turn off too many readers. I will give each equation in both a simple text format and in proper LaTeX. Remember, you can render LaTeX here.

PD = PR – 1/e * Q

P_D = P_R – \frac{1}{e} Q \\

The marginal cost that landlords have to pay, the supply price PS, is a bit weirder, as I’ll talk about more in a moment. For now let’s say that it is a linear function, starting at zero cost for some quantity Q0 and then increases linearly according to a parameter n that similarly represents the elasticity of supply.

PS = 1/n * (Q – Q0)

P_S = \frac{1}{n} \left( Q – Q_0 \right) \\

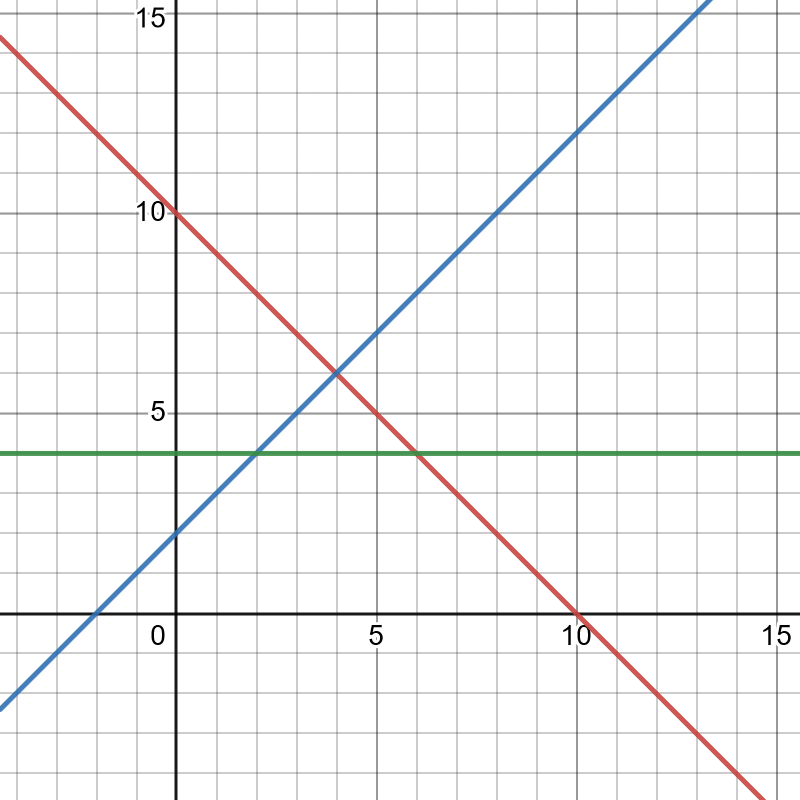
Now, if you introduce a tax, there will be a difference between the price that renters pay and the price that landlords receive—namely, the tax, which we’ll call T. I’m going to assume that, on paper, the landlord pays the whole tax. As I said above, this literally does not matter. I could assume that on paper the renter pays the whole tax, and the real effect on the distribution of wealth would be identical. All we’d have to do is set PD = P and PS = P – T; the consumer and producer surplus would end up exactly the same. Or we could do something in between, with P’D = P + rT and P’S = P – (1 – r) T.

Then, if the market is competitive, we just set the prices equal, taking the tax into account:

P = PD – T = PR – 1/e * Q – T = PS = 1/n * (Q – Q0)

P= P_D – T = P_R – \frac{1}{e} Q – T= P_S = \frac{1}{n} \left(Q – Q_0 \right) \\

P_R – 1/e * Q – T = 1/n * (Q – Q0)

P_R – \frac{1}{e} Q – T = \frac{1}{n} \left(Q – Q_0 \right) \\

Notice the equivalency here; if we set P’D = P + rT and P’S = P – (1 – r) T, so that the consumer now pays a fraction of the tax r.

P = P’D – rT = P_r – 1/e*Q = P’S + (1 – r) T + 1/n * (Q – Q0) + (1 – r) T

P^\prime_D – r T = P = P_R – \frac{1}{e} Q = P^\prime_S = \frac{1}{n} \left(Q – Q_0 \right) + (1 – r) T\\

The result is exactly the same:

P_R – 1/e * Q – T = 1/n * (Q – Q0)

P_R – \frac{1}{e} Q – T = \frac{1}{n} \left(Q – Q_0 \right) \\

I’ll spare you the algebra, but this comes out to:

Q = (PR – T)/(1/n + 1/e) + (Q0)/(1 + n/e)

Q = \frac{P_R – T}{\frac{1}{n} + \frac{1}{e}} + \frac{Q_0}{1 + \frac{n}{e}}

P = (PR – T)/(1+ n/e) – (Q0)/(e + n)

P = \frac{P_R – T}}{1 + \frac{n}{e}} – \frac{Q_0}{e+n} \\

That’s if the market is competitive.

If the market is a monopoly, instead of setting the prices equal, we set the price the landlord receives equal to the marginal revenue—which takes into account the fact that increasing the amount they sell forces them to reduce the price they charge everyone else. Thus, the marginal revenue drops faster than the price as the quantity sold increases.

After a bunch of algebra (and just a dash of calculus), that comes out to these very similar, but not quite identical, equations:

Q = (PR – T)/(1/n + 2/e) + (Q0)/(1+ 2n/e)

Q = \frac{P_R – T}{\frac{1}{n} + \frac{2}{e}} + \frac{Q_0}{1 + \frac{2n}{e}} \\

P = (PR – T)*((1/n + 1/e)/(1/n + 2/e) – (Q0)/(e + 2n)

P = \left( P_R – T\right)\frac{\frac{1}{n} + \frac{1}{e}}{\frac{1}{n} + \frac{2}{e}} – \frac{Q_0}{e+2n} \\

Yes, it changes some 1s into 2s. That by itself accounts for the full effect of monopoly. That’s why I think it’s worthwhile to use the equations; they are deeply elegant and express in a compact form all of the different cases. They look really intimidating right now, but for most of the cases we’ll consider these general equations simplify quite dramatically.

There are several cases to consider.

Land has an extremely high cost to create—for practical purposes, we can consider its supply fixed, that is, perfectly inelastic. If the market is competitive, so that landlords have no market power, then they will simply rent out all the land they have at whatever price the market will bear:

Inelastic_supply_competitive_labeled

This is like setting n = 0 and T = 0 in the above equations, the competitive ones.

Q = Q0

Q = Q_0 \\

P = PR – Q0/e

P = P_R – \frac{Q_0}{e} \\

If we now introduce a tax, it will fall completely on the landlords, because they have little choice but to rent out all the land they have, and they can only rent it at a price—including tax—that the market will bear.

inelastic_supply_competitive_tax_labeled

Now we still have n = 0 but not T = 0.

Q = Q0

Q = Q_0 \\

P = PR – T – Q0/e

P = P_R – T – \frac{Q_0}{e} \\

The consumer surplus will be:

½ (Q)(PR – P – T) = 1/(2e)* Q02

\frac{1}{2}Q(P_R – P – T) = \frac{1}{2e}Q_0^2 \\

Notice how T isn’t in the result. The consumer surplus is unaffected by the tax.

The producer surplus, on the other hand, will be reduced by the tax:

(Q)(P) = (PR – T – Q0/e) Q0 = PR Q0 – 1/e Q02 – TQ0

(Q)(P) = (P_R – T – \frac{Q_0}{e})Q_0 = P_R Q_0 – \frac{1}{e} Q_0^2 – T Q_0 \\

T appears linearly as TQ0, which is the same as the tax revenue. All the money goes directly from the landlord to the government, as we want if our goal is to redistribute wealth without raising rent.

But now suppose that the market is not competitive, and by tacit collusion or regulatory capture the landlords can exert some market power; this is quite likely the case in reality. Actually in reality we’re probably somewhere in between monopoly and competition, either oligopoly or monopolistic competition—which I will talk about a good deal more in a later post, I promise.

It could be that demand is still sufficiently high that even with their market power, landlords have an incentive to rent out all their available land, in which case the result will be the same as in the competitive market.

inelastic_supply_monopolistic_labeled

A tax will then fall completely on the landlords as before:

inelastic_supply_monopolistic_tax_labeled

Indeed, in this case it doesn’t really matter that the market is monopolistic; everything is the same as it would be under a competitive market. Notice how if you set n = 0, the monopolistic equations and the competitive equations come out exactly the same. The good news is, this is quite likely our actual situation! So even in the presence of significant market power the land tax can redistribute wealth in just the way we want.

But there are a few other possibilities. One is that demand is not sufficiently high, so that the landlords’ market power causes them to actually hold back some land in order to raise the price:

zerobound_supply_monopolistic_labeled

This will create some of what we call deadweight loss, in which some economic value is wasted. By restricting the land they rent out, the landlords make more profit, but the harm they cause to tenant is created than the profit they gain, so there is value wasted.

Now instead of setting n = 0, we actually set n = infinity. Why? Because the reason that the landlords restrict the land they sell is that their marginal revenue is actually negative beyond that point—they would actually get less money in total if they sold more land. Instead of being bounded by their cost of production (because they have none, the land is there whether they sell it or not), they are bounded by zero. (Once again we’ve hit upon a fundamental concept in economics, particularly macroeconomics, that I don’t have time to talk about today: the zero lower bound.) Thus, they can change quantity all they want (within a certain range) without changing the price, which is equivalent to a supply elasticity of infinity.

Introducing a tax will then exacerbate this deadweight loss (adding DWL2 to the original DWL1), because it provides even more incentive for the landlords to restrict the supply of land:

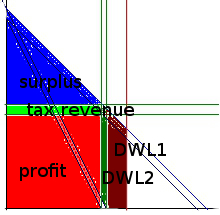
zerobound_supply_monopolistic_tax_labeled

Q = e/2*(PR – T)

Q = \frac{e}{2} \left(P_R – T\right)\\

P = 1/2*(PR – T)

P = \frac{1}{2} \left(P_R – T\right) \\

The quantity Q0 completely drops out, because it doesn’t matter how much land is available (as long as it’s enough); it only matters how much land it is profitable to rent out.

We can then find the consumer and producer surplus, and see that they are both reduced by the tax. The consumer surplus is as follows:

½ (Q)(PR – 1/2(PR – T)) = e/4*(PR2 – T2)

\frac{1}{2}Q \left( P_R – \frac{1}{2}left( P – T \right) \right) = \frac{e}{4}\left( P_R^2 – T^2 \right) \\

This time, the tax does have an effect on reducing the consumer surplus.

The producer surplus, on the other hand, will be:

(Q)(P) = 1/2*(PR – T)*e/2*(PR – T) = e/4*(PR – T)2

(Q)(P) = \frac{1}{2}\left(P_R – T \right) \frac{e}{2} \left(P_R – T\right) = \frac{e}{4} \left(P_R – T)^2 \\

Notice how it is also reduced by the tax—and no longer in a simple linear way.

The tax revenue is now a function of the demand:

TQ = e/2*T(PR – T)

T Q = \frac{e}{2} T (P_R – T) \\

If you add all these up, you’ll find that the sum is this:

e/2 * (PR^2 – T^2)

\frac{e}{2} \left(P_R^2 – T^2 \right) \\

The sum is actually reduced by an amount equal to e/2*T^2, which is the deadweight loss.

Finally there is an even worse scenario, in which the tax is so large that it actually creates an incentive to restrict land where none previously existed:

zerobound_supply_monopolistic_hugetax_labeled

Notice, however, that because the supply of land is inelastic the deadweight loss is still relatively small compared to the huge amount of tax revenue.

But actually this isn’t the whole story, because a land tax provides an incentive to get rid of land that you’re not profiting from. If this incentive is strong enough, the monopolistic power of landlords will disappear, as the unused land gets sold to more landholders or to the government. This is a way of avoiding the tax, but it’s one that actually benefits society, so we don’t mind incentivizing it.

Now, let’s compare this to our current system of property taxes, which include the value of buildings. Buildings are expensive to create, but we build them all the time; the supply of buildings is strongly dependent upon the price at which those buildings will sell. This makes for a supply curve that is somewhat elastic.

If the market were competitive and we had no taxes, it would be optimally efficient:

elastic_supply_competitive_labeled

Property taxes create an incentive to produce fewer buildings, and this creates deadweight loss. Notice that this happens even if the market is perfectly competitive:

elastic_supply_competitive_tax_labeled

Since both n and e are finite and nonzero, we’d need to use the whole equations: Since the algebra is such a mess, I don’t see any reason to subject you to it; but suffice it to say, the T does not drop out. Tenants do see their consumer surplus reduced, and the larger the tax the more this is so.

Now, suppose that the market for buildings is monopolistic, as it most likely is. This would create deadweight loss even in the absence of a tax:

elastic_supply_monopolistic_labeled

But a tax will add even more deadweight loss:

elastic_supply_monopolistic_tax_labeled

Once again, we’d need the full equations, and once again it’s a mess; but the result is, as before, that the tax gets passed on to the tenants in the form of more restricted sales and therefore higher rents.

Because of the finite supply elasticity, there’s no way that the tax can avoid raising the rent. As long as landlords have to pay more taxes when they build more or better buildings, they are going to raise the rent in those buildings accordingly—whether the market is competitive or not.

If the market is indeed monopolistic, there may be ways to bring the rent down: suppose we know what the competitive market price of rent should be, and we can establish rent control to that effect. If we are truly correct about the price to set, this rent control can not only reduce rent, it can actually reduce the deadweight loss:

effective_rent_control_tax_labeled

But if we set the rent control too low, or don’t properly account for the varying cost of different buildings, we can instead introduce a new kind of deadweight loss, by making it too expensive to make new buildings.

ineffective_rent_control_tax_labeled

In fact, what actually seems to happen is more complicated than that—because otherwise the number of buildings is obviously far too small, rent control is usually set to affect some buildings and not others. So what seems to happen is that the rent market fragments into two markets: One, which is too small, but very good for those few who get the chance to use it; and the other, which is unaffected by the rent control but is more monopolistic and therefore raises prices even further. This is why almost all economists are opposed to rent control (PDF); it doesn’t solve the problem of high rent and simply causes a whole new set of problems.

A land tax with a basic income, on the other hand, would help poor people at least as much as rent control presently does—probably a good deal more—without discouraging the production and maintenance of new apartment buildings.

But now we come to a key point: The land tax must be uniform per hectare.

If it is instead based on the value of the land, then this acts like a finite elasticity of supply; it provides an incentive to reduce the value of your own land in order to avoid the tax. As I showed above, this is particularly pernicious if the market is monopolistic, but even if it is competitive the effect is still there.

One exception I can see is if there are different tiers based on broad classes of land that it’s difficult to switch between, such as “land in Manhattan” versus “land in Brooklyn” or “desert land” versus “forest land”. But even this policy would have to be done very carefully, because any opportunity to substitute can create an opportunity to pass on the tax to someone else—for instance if land taxes are lower in Brooklyn developers are going to move to Brooklyn. Maybe we want that, in which case that is a good policy; but we should be aware of these sorts of additional consequences. The simplest way to avoid all these problems is to simply make the land tax uniform. And given the quantities we’re talking about—less than $3000 per hectare per year—it should be affordable for anyone except the very large landholders we’re trying to distribute wealth from in the first place.

The good news is, most economists would probably be on board with this proposal. After all, the neoclassical models themselves say it would be more efficient than our current system of rent control and property taxes—and the idea is at least as old as Adam Smith. Perhaps we can finally change the fact that the rent is too damn high.